Advertisements
Advertisements
प्रश्न
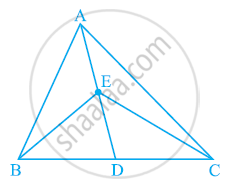
In the given figure, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar (ACE)
उत्तर
AD is the median of ΔABC. Therefore, it will divide ΔABC into two triangles of equal areas.
∴ Area (ΔABD) = Area (ΔACD) ... (1)
ED is the median of ΔEBC.
∴ Area (ΔEBD) = Area (ΔECD) ... (2)
On subtracting equation (2) from equation (1), we obtain
Area (ΔABD) − Area (EBD) = Area (ΔACD) − Area (ΔECD)
Area (ΔABE) = Area (ΔACE)
APPEARS IN
संबंधित प्रश्न
In the given figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB or ABCD is a parallelogram.
[Hint: From D and B, draw perpendiculars to AC.]

D and E are points on sides AB and AC respectively of ΔABC such that
ar (DBC) = ar (EBC). Prove that DE || BC.
A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
In the given figure, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).

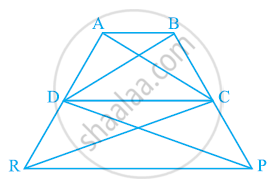
In the given figure, ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (APB) × ar (CPD) = ar (APD) × ar (BPC).
[Hint : From A and C, draw perpendiculars to BD.]
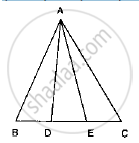
In the below fig. D and E are two points on BC such that BD = DE = EC. Show that ar
(ΔABD) = ar (ΔADE) = ar (ΔAEC).
PQRS is a parallelogram whose area is 180 cm2 and A is any point on the diagonal QS. The area of ∆ASR = 90 cm2.
The medians BE and CF of a triangle ABC intersect at G. Prove that the area of ∆GBC = area of the quadrilateral AFGE.
If the medians of a ∆ABC intersect at G, show that ar (AGB) = ar (AGC) = ar (BGC) = `1/3` ar (ABC)
