Advertisements
Advertisements
प्रश्न
In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
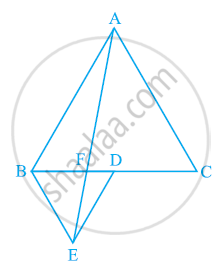
(i) ar (BDE) = 1/4 ar (ABC)
(ii) ar (BDE) = 1/2 ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 1/8 ar (AFC)
[Hint : Join EC and AD. Show that BE || AC and DE || AB, etc.]
उत्तर
(i) Let G and H be the mid-points of side AB and AC respectively.
Line segment GH is joining the mid-points. Therefore, it will be parallel to third side BC and also its length will be half of the length of BC (mid-point theorem).
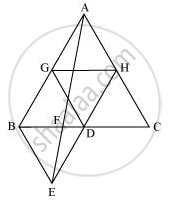
⇒ GH = 1/2BC and GH || BD
⇒ GH = BD = DC and GH || BD (D is the mid-point of BC)
Consider quadrilateral GHDB.
GH ||BD and GH = BD
Two line segments joining two parallel line segments of equal length will also be equal and parallel to each other.
Therefore, BG = DH and BG || DH
Hence, quadrilateral GHDB is a parallelogram.
We know that in a parallelogram, the diagonal bisects it into two triangles of equal area.
Hence, Area (ΔBDG) = Area (ΔHGD)
Similarly, it can be proved that quadrilaterals DCHG, GDHA, and BEDG are parallelograms and their respective diagonals are dividing them into two triangles of equal area.
ar (ΔGDH) = ar (ΔCHD) (For parallelogram DCHG)
ar (ΔGDH) = ar (ΔHAG) (For parallelogram GDHA)
ar (ΔBDE) = ar (ΔDBG) (For parallelogram BEDG)
ar (ΔABC) = ar(ΔBDG) + ar(ΔGDH) + ar(ΔDCH) + ar(ΔAGH)
ar (ΔABC) = 4 × ar(ΔBDE)
Hence, ar(BDE) = 1/4 ar(ABC)
(ii) Area (ΔBDE) = Area (ΔAED) (Common base DE and DE||AB)
Area (ΔBDE) − Area (ΔFED) = Area (ΔAED) − Area (ΔFED)
Area (ΔBEF) = Area (ΔAFD) (1)
Area (ΔABD) = Area (ΔABF) + Area (ΔAFD)
Area (ΔABD) = Area (ΔABF) + Area (ΔBEF) [From equation (1)]
Area (ΔABD) = Area (ΔABE) (2)
AD is the median in ΔABC.
`ar(ΔABD) = 1/2 ar(ΔABC)`
`= 1/4ar(ΔBDE)" (as proved earlier)"`
`ar(ΔABD) = 2ar(ΔBDE)" ........(3)"`
From (2) and (3), we obtain
2 ar (ΔBDE) = ar (ΔABE)
Or, ar(ΔBDE) = 1/2ar(ΔABE)
(iii)
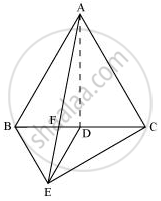
ar (ΔABE) = ar (ΔBEC) (Common base BE and BE||AC)
ar (ΔABF) + ar (ΔBEF) = ar (ΔBEC)
Using equation (1), we obtain
ar (ΔABF) + ar (ΔAFD) = ar (ΔBEC)
ar (ΔABD) = ar (ΔBEC)
1/2 ar(ΔABC) = ar(ΔBEC)
ar (ΔABC) = 2 ar (ΔBEC)
(iv) It is seen that ΔBDE and ar ΔAED lie on the same base (DE) and between the parallels DE and AB.
∴ ar (ΔBDE) = ar (ΔAED)
⇒ ar (ΔBDE) − ar (ΔFED) = ar (ΔAED) − ar (ΔFED)
∴ ar (ΔBFE) = ar (ΔAFD)
(v) Let h be the height of vertex E, corresponding to the side BD in ΔBDE.
Let H be the height of vertex A, corresponding to the side BC in ΔABC.
In (i), it was shown that ar(BDE) = 1/4ar(ABC).
`therefore1/2xxBDxxh=1/4(1/2xxBCxxH)`
`rArrBDxxh=1/4(2BDxxH)`
`rArrh=1/2H`
In (iv), it was shown that ar (ΔBFE) = ar (ΔAFD).
∴ ar (ΔBFE) = ar (ΔAFD)
`=1/2xxFDxxH=1/2xxFDxx2h=2(1/2xxFDxxh)`
= 2 ar (ΔFED)
`"Hence, "ar(BFE) = 2ar(FED)`
(vi) Area (AFC) = area (AFD) + area (ADC)
`=ar(BFE)+1/2ar(ABC)" "["In (iv), "ar(BFE) = ar(AFD);" AD is median of ΔABC"]`
`=ar(BFE)+1/2xx4ar(BDE)" "["In (i), "ar(BDE)=1/4ar(ABC)]" Now, by (v),"`
= ar(BFE) + 2ar(BDE) ............(5)
ar(BFE) = 2ar(FED) ...........(6)
ar(BDE) = ar(BFE) + ar(FED) = 2ar(FED) + ar(FED) = 3ar(FED) .........(7)
Therefore, from equations (5), (6), and (7), we get:
ar(AFC) = 2ar(FED) + 2 x 3ar(FED) = 8ar(FED)
∴ ar(AFC) = 8ar(FED)
`Hence, ar(FED) = 1/8ar(AFC)`
APPEARS IN
संबंधित प्रश्न
In a triangle ABC, E is the mid-point of median AD. Show that ar (BED) = 1/4ar (ABC).
In the given figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB or ABCD is a parallelogram.
[Hint: From D and B, draw perpendiculars to AC.]

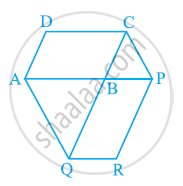
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see the following figure). Show that
ar (ABCD) = ar (PBQR).
[Hint: Join AC and PQ. Now compare area (ACQ) and area (APQ)]
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (APB) × ar (CPD) = ar (APD) × ar (BPC).
[Hint : From A and C, draw perpendiculars to BD.]
In the following figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:-
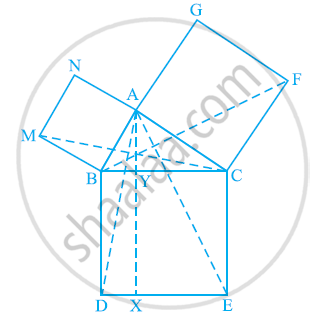
(i) ΔMBC ≅ ΔABD
(ii) ar (BYXD) = 2 ar(MBC)
(iii) ar (BYXD) = ar(ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2 ar(FCB)
(vi) ar (CYXE) = ar(ACFG)
(vii) ar (BCED) = ar(ABMN) + ar(ACFG)
Note : Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class X.
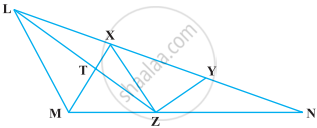
X and Y are points on the side LN of the triangle LMN such that LX = XY = YN. Through X, a line is drawn parallel to LM to meet MN at Z (See figure). Prove that ar (LZY) = ar (MZYX)
If the medians of a ∆ABC intersect at G, show that ar (AGB) = ar (AGC) = ar (BGC) = `1/3` ar (ABC)
