Advertisements
Advertisements
Question
In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
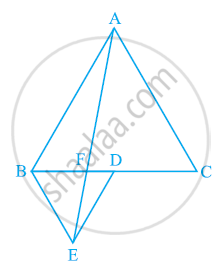
(i) ar (BDE) = 1/4 ar (ABC)
(ii) ar (BDE) = 1/2 ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 1/8 ar (AFC)
[Hint : Join EC and AD. Show that BE || AC and DE || AB, etc.]
Solution
(i) Let G and H be the mid-points of side AB and AC respectively.
Line segment GH is joining the mid-points. Therefore, it will be parallel to third side BC and also its length will be half of the length of BC (mid-point theorem).
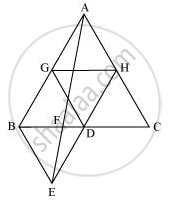
⇒ GH = 1/2BC and GH || BD
⇒ GH = BD = DC and GH || BD (D is the mid-point of BC)
Consider quadrilateral GHDB.
GH ||BD and GH = BD
Two line segments joining two parallel line segments of equal length will also be equal and parallel to each other.
Therefore, BG = DH and BG || DH
Hence, quadrilateral GHDB is a parallelogram.
We know that in a parallelogram, the diagonal bisects it into two triangles of equal area.
Hence, Area (ΔBDG) = Area (ΔHGD)
Similarly, it can be proved that quadrilaterals DCHG, GDHA, and BEDG are parallelograms and their respective diagonals are dividing them into two triangles of equal area.
ar (ΔGDH) = ar (ΔCHD) (For parallelogram DCHG)
ar (ΔGDH) = ar (ΔHAG) (For parallelogram GDHA)
ar (ΔBDE) = ar (ΔDBG) (For parallelogram BEDG)
ar (ΔABC) = ar(ΔBDG) + ar(ΔGDH) + ar(ΔDCH) + ar(ΔAGH)
ar (ΔABC) = 4 × ar(ΔBDE)
Hence, ar(BDE) = 1/4 ar(ABC)
(ii) Area (ΔBDE) = Area (ΔAED) (Common base DE and DE||AB)
Area (ΔBDE) − Area (ΔFED) = Area (ΔAED) − Area (ΔFED)
Area (ΔBEF) = Area (ΔAFD) (1)
Area (ΔABD) = Area (ΔABF) + Area (ΔAFD)
Area (ΔABD) = Area (ΔABF) + Area (ΔBEF) [From equation (1)]
Area (ΔABD) = Area (ΔABE) (2)
AD is the median in ΔABC.
`ar(ΔABD) = 1/2 ar(ΔABC)`
`= 1/4ar(ΔBDE)" (as proved earlier)"`
`ar(ΔABD) = 2ar(ΔBDE)" ........(3)"`
From (2) and (3), we obtain
2 ar (ΔBDE) = ar (ΔABE)
Or, ar(ΔBDE) = 1/2ar(ΔABE)
(iii)
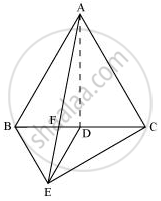
ar (ΔABE) = ar (ΔBEC) (Common base BE and BE||AC)
ar (ΔABF) + ar (ΔBEF) = ar (ΔBEC)
Using equation (1), we obtain
ar (ΔABF) + ar (ΔAFD) = ar (ΔBEC)
ar (ΔABD) = ar (ΔBEC)
1/2 ar(ΔABC) = ar(ΔBEC)
ar (ΔABC) = 2 ar (ΔBEC)
(iv) It is seen that ΔBDE and ar ΔAED lie on the same base (DE) and between the parallels DE and AB.
∴ ar (ΔBDE) = ar (ΔAED)
⇒ ar (ΔBDE) − ar (ΔFED) = ar (ΔAED) − ar (ΔFED)
∴ ar (ΔBFE) = ar (ΔAFD)
(v) Let h be the height of vertex E, corresponding to the side BD in ΔBDE.
Let H be the height of vertex A, corresponding to the side BC in ΔABC.
In (i), it was shown that ar(BDE) = 1/4ar(ABC).
`therefore1/2xxBDxxh=1/4(1/2xxBCxxH)`
`rArrBDxxh=1/4(2BDxxH)`
`rArrh=1/2H`
In (iv), it was shown that ar (ΔBFE) = ar (ΔAFD).
∴ ar (ΔBFE) = ar (ΔAFD)
`=1/2xxFDxxH=1/2xxFDxx2h=2(1/2xxFDxxh)`
= 2 ar (ΔFED)
`"Hence, "ar(BFE) = 2ar(FED)`
(vi) Area (AFC) = area (AFD) + area (ADC)
`=ar(BFE)+1/2ar(ABC)" "["In (iv), "ar(BFE) = ar(AFD);" AD is median of ΔABC"]`
`=ar(BFE)+1/2xx4ar(BDE)" "["In (i), "ar(BDE)=1/4ar(ABC)]" Now, by (v),"`
= ar(BFE) + 2ar(BDE) ............(5)
ar(BFE) = 2ar(FED) ...........(6)
ar(BDE) = ar(BFE) + ar(FED) = 2ar(FED) + ar(FED) = 3ar(FED) .........(7)
Therefore, from equations (5), (6), and (7), we get:
ar(AFC) = 2ar(FED) + 2 x 3ar(FED) = 8ar(FED)
∴ ar(AFC) = 8ar(FED)
`Hence, ar(FED) = 1/8ar(AFC)`
APPEARS IN
RELATED QUESTIONS
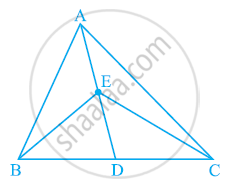
In the given figure, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar (ACE)
D and E are points on sides AB and AC respectively of ΔABC such that
ar (DBC) = ar (EBC). Prove that DE || BC.
XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that
ar (ABE) = ar (ACF)
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see the following figure). Show that
ar (ABCD) = ar (PBQR).
[Hint: Join AC and PQ. Now compare area (ACQ) and area (APQ)]
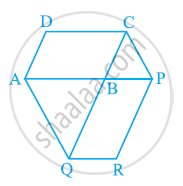
In the given figure, ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
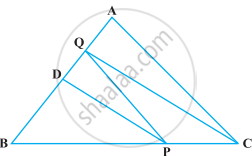
In ∆ABC, D is the mid-point of AB and P is any point on BC. If CQ || PD meets AB in Q (Figure), then prove that ar (BPQ) = `1/2` ar (∆ABC).
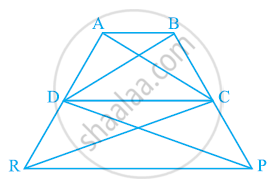
The medians BE and CF of a triangle ABC intersect at G. Prove that the area of ∆GBC = area of the quadrilateral AFGE.
In ∆ABC, if L and M are the points on AB and AC, respectively such that LM || BC. Prove that ar (LOB) = ar (MOC)
If the medians of a ∆ABC intersect at G, show that ar (AGB) = ar (AGC) = ar (BGC) = `1/3` ar (ABC)
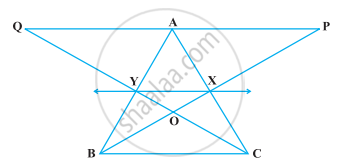
In the following figure, X and Y are the mid-points of AC and AB respectively, QP || BC and CYQ and BXP are straight lines. Prove that ar (ABP) = ar (ACQ).