Advertisements
Advertisements
प्रश्न
In the following figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:-
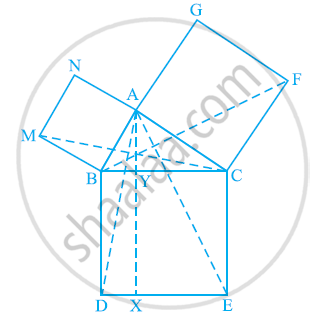
(i) ΔMBC ≅ ΔABD
(ii) ar (BYXD) = 2 ar(MBC)
(iii) ar (BYXD) = ar(ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2 ar(FCB)
(vi) ar (CYXE) = ar(ACFG)
(vii) ar (BCED) = ar(ABMN) + ar(ACFG)
Note : Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class X.
उत्तर
(i) We know that each angle of a square is 90°.
Hence, ∠ABM = ∠DBC = 90º
⇒ ∠ABM + ∠ABC = ∠DBC + ∠ABC
⇒ ∠MBC = ∠ABD
In ΔMBC and ΔABD,
∠MBC = ∠ABD (Proved above)
MB = AB (Sides of square ABMN)
BC = BD (Sides of square BCED)
∴ ΔMBC ≅ ΔABD (SAS congruence rule)
(ii) We have
ΔMBC ≅ ΔABD
⇒ ar (ΔMBC) = ar (ΔABD) ... (1)
It is given that AX ⊥ DE and BD ⊥ DE (Adjacent sides of square
BDEC)
⇒ BD || AX (Two lines perpendicular to same line are parallel to each other)
ΔABD and parallelogram BYXD are on the same base BD and between the same parallels BD and AX.
∴ ar(ΔABD) = 1/2ar(BYXD)
ar(BYXD) = 2ar(ΔABD)
Area (BYXD) = 2 area (ΔMBC) [Using equation (1)] ... (2)
(iii) ΔMBC and parallelogram ABMN are lying on the same base MB and between same parallels MB and NC.
∴ ar(ΔMBC) = 1/2ar(ABMN)
2ar (ΔMBC) = ar (ABMN)
ar (BYXD) = ar (ABMN) [Using equation (2)] ... (3)
(iv) We know that each angle of a square is 90°.
∴ ∠FCA = ∠BCE = 90º
⇒ ∠FCA + ∠ACB = ∠BCE + ∠ACB
⇒ ∠FCB = ∠ACE
In ΔFCB and ΔACE,
∠FCB = ∠ACE
FC = AC (Sides of square ACFG)
CB = CE (Sides of square BCED)
ΔFCB ≅ ΔACE (SAS congruence rule)
(v) It is given that AX ⊥ DE and CE ⊥ DE (Adjacent sides of square BDEC)
Hence, CE || AX (Two lines perpendicular to the same line are parallel to each other)
Consider ΔACE and parallelogram CYXE
ΔACE and parallelogram CYXE are on the same base CE and between the same parallels CE and AX.
∴ ar(ΔACE) = 1/2ar(CYXE)
⇒ ar(CYXE) = 2 ar(ΔACE) ... (4)
We had proved that
∴ ΔFCB ≅ ΔACE
ar (ΔFCB) ≅ ar (ΔACE) ... (5)
On comparing equations (4) and (5), we obtain
ar (CYXE) = 2 ar (ΔFCB) ... (6)
(vi) Consider ΔFCB and parallelogram ACFG
ΔFCB and parallelogram ACFG are lying on the same base CF and between the same parallels CF and BG.
∴ ar(ΔFCB) = 1/2 ar(ACFG)
⇒ ar(ACFG) = 2 ar(ΔFCB)
⇒ ar (ACFG) = ar (CYXE) [Using equation (6)] ... (7)
(vii) From the figure, it is evident that
ar (BCED) = ar (BYXD) + ar (CYXE)
⇒ ar (BCED) = ar (ABMN) + ar (ACFG) [Using equations (3) and (7)]
APPEARS IN
संबंधित प्रश्न
XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that
ar (ABE) = ar (ACF)
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see the following figure). Show that
ar (ABCD) = ar (PBQR).
[Hint: Join AC and PQ. Now compare area (ACQ) and area (APQ)]
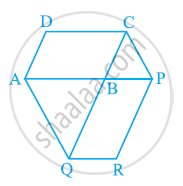
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
In the given figure, ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
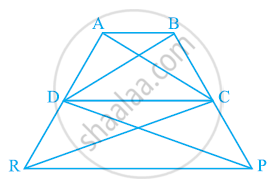
P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
(i) ar(PRQ) = 1/2 ar(ARC)
(ii) ar(RQC) = 3/8 ar(ABC)
(iii) ar(PBQ) = ar(ARC)
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE) = `1/4` ar (ABC).
The area of the parallelogram ABCD is 90 cm2 (see figure). Find ar (ΔBEF)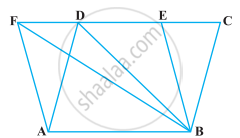
A point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar (ADF) = ar (ABFC)
In the following figure, CD || AE and CY || BA. Prove that ar (CBX) = ar (AXY).

In the following figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar (ABCDE) = ar (APQ)