Advertisements
Advertisements
प्रश्न
P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
(i) ar(PRQ) = 1/2 ar(ARC)
(ii) ar(RQC) = 3/8 ar(ABC)
(iii) ar(PBQ) = ar(ARC)
उत्तर
Take a point S on AC such that S is the mid-point of AC.
Extend PQ to T such that PQ = QT.
Join TC, QS, PS, and AQ.
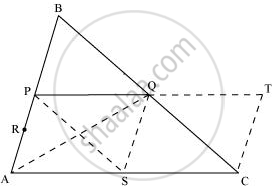
In ΔABC, P and Q are the mid-points of AB and BC respectively. Hence, by using mid-point theorem, we obtain
PQ || AC and PQ = 1/2AC
⇒ PQ || AS and PQ = AS (As S is the mid-point of AC)
∴ PQSA is a parallelogram. We know that diagonals of a parallelogram bisect it into equal areas of triangles.
∴ ar (ΔPAS) = ar (ΔSQP) = ar (ΔPAQ) = ar (ΔSQA)
Similarly, it can also be proved that quadrilaterals PSCQ, QSCT, and PSQB are also parallelograms and therefore,
ar (ΔPSQ) = ar (ΔCQS) (For parallelogram PSCQ)
ar (ΔQSC) = ar (ΔCTQ) (For parallelogram QSCT)
ar (ΔPSQ) = ar (ΔQBP) (For parallelogram PSQB)
Thus,
ar (ΔPAS) = ar (ΔSQP) = ar (ΔPAQ) = ar (ΔSQA) = ar (ΔQSC) = ar (ΔCTQ) = ar (ΔQBP) ... (1)
Also, ar (ΔABC) = ar (ΔPBQ) + ar (ΔPAS) + ar (ΔPQS) + ar (ΔQSC)
ar (ΔABC) = ar (ΔPBQ) + ar (ΔPBQ) + ar (ΔPBQ) + ar (ΔPBQ)
= 4 ar (ΔPBQ)
⇒ ar (ΔPBQ) = 1/4 ar(ΔABC) ... (2)
(i)Join point P to C.
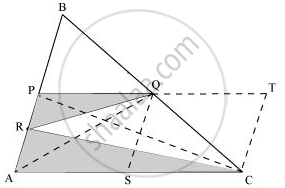
In ΔPAQ, QR is the median.
`therefore ar(trianglePRQ)=1/2ar(trianglePAQ)=1/2xx1/4ar(triangleABC)=1/8ar(triangleABC)" .........(3)"`
In ΔABC, P and Q are the mid-points of AB and BC respectively. Hence, by using mid-point theorem, we obtain
PQ = 1/2AC
AC = 2PQ ⇒ AC = PT
Also, PQ || AC ⇒ PT || AC
Hence, PACT is a parallelogram.
ar (PACT) = ar (PACQ) + ar (ΔQTC)
= ar (PACQ) + ar (ΔPBQ [Using equation (1)]
∴ ar (PACT) = ar (ΔABC) ... (4)
`ar(triangleARC) = 1/2ar(trianglePAC)" (CR is the median of ΔPAC)"`
`= 1/2xx1/2ar(PACT)" (PC is the diagonal parallelogram PACT)"`
`= 1/4 ar(PACT) = 1/4 ar(triangleABC)`
`rArr 1/2ar(triangleARC) = 1/8ar(triangleABC)`
`rArr1/2ar(triangleARC)=ar(trianglePRQ)" [Using equation (3)] .......(5)"`
(ii)
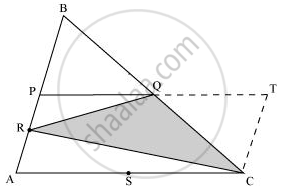
ar(PACT) = ar(ΔPRQ) + ar(ΔARC) + ar(ΔQTC) + ar(ΔRQC)
Putting the values from equations (1), (2), (3), (4), and (5), we obtain
`ar(ΔABC) = 1/8ar(ΔABC) + 1/4ar(ΔABC) + 1/4ar(ΔABC) + ar(ΔRQC)`
`ar(ΔABC) = 5/8ar(ΔABC) + ar(ΔRQC)`
`ar(ΔRQC) = (1-5/8)ar(ΔABC)`
`ar(ΔRQC) = 3/8ar(ΔABC)`
(iii) In parallelogram PACT,
`ar(ΔARC) = 1/2ar(ΔPAC)" (CR is the median of ΔPAC)"`
`= 1/2xx1/2ar(PACT)" (PC is the diagonal of parallelogram PACT)"`
`= 1/4ar(PACT)`
`= 1/4ar(ABC)`
= ar(ΔPBQ)
APPEARS IN
संबंधित प्रश्न
In the given figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB or ABCD is a parallelogram.
[Hint: From D and B, draw perpendiculars to AC.]

D and E are points on sides AB and AC respectively of ΔABC such that
ar (DBC) = ar (EBC). Prove that DE || BC.
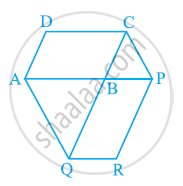
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see the following figure). Show that
ar (ABCD) = ar (PBQR).
[Hint: Join AC and PQ. Now compare area (ACQ) and area (APQ)]
In the following figure, D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) = ar (AEC).
Can you answer the question that you have left in the ’Introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?
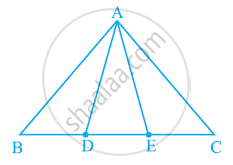
[Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide ΔABC into n triangles of equal areas.]
In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
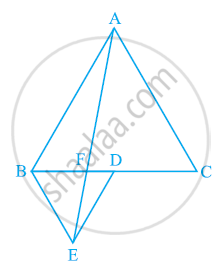
(i) ar (BDE) = 1/4 ar (ABC)
(ii) ar (BDE) = 1/2 ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 1/8 ar (AFC)
[Hint : Join EC and AD. Show that BE || AC and DE || AB, etc.]
In a ΔABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point
of AP. Prove that :
(1) ar (Δ PBQ) = ar (Δ ARC)
(2) ar (Δ PRQ) =`1/2`ar (Δ ARC)
(3) ar (Δ RQC) =`3/8` ar (Δ ABC) .
In a ΔABC, if L and M are points on AB and AC respectively such that LM || BC. Prove
that:
(1) ar (ΔLCM ) = ar (ΔLBM )
(2) ar (ΔLBC) = ar (ΔMBC)
(3) ar (ΔABM) ar (ΔACL)
(4) ar (ΔLOB) ar (ΔMOC)
If a triangle and a parallelogram are on the same base and between same parallels, then the ratio of the area of the triangle to the area of parallelogram is ______.
ABCD is a parallelogram and X is the mid-point of AB. If ar (AXCD) = 24 cm2, then ar (ABC) = 24 cm2.
In ∆ABC, if L and M are the points on AB and AC, respectively such that LM || BC. Prove that ar (LOB) = ar (MOC)
