Advertisements
Advertisements
प्रश्न
ABCD is a trapezium in which AB || DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that ar (DCYX) = `7/9` ar (XYBA)
उत्तर
Given: In a trapezium ABCD, AB || DC, DC = 30 cm and AB = 50 cm.
Also, X and Y are respectively the mid-points of AD and BC.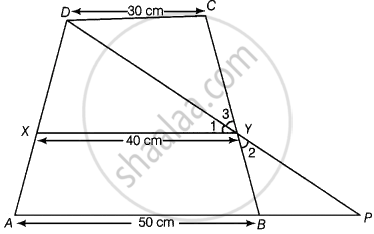
To prove: `ar (DCYX) = 7/9 ar (XYBA)`
Construction: Join DY and extend it to meet produced AB at P.
Proof: In ΔDCY and ΔPBY,
CY = BY ...[Since, Y is the mid-point of BC]
∠DCY = ∠PBY ...[Alternate interior angles]
And ∠2 = ∠3 ...[Vertically opposite angles]
∴ ΔDCY ≅ ΔPBY ...[By ASA congruence rule]
Then, DC = BP ...[By CPCT]
But DC = 30 cm ...[Given]
∴ DC = BP = 30 cm
Now, AP = AB + BP
= 50 + 30
= 80 cm
In ΔADP, by mid-point theorem,
`XY = 1/2 AP`
= `1/2 xx 80`
= 40 cm
Let distance between AB, XY and XY, DC is h cm.
Now, area of trapezium `DCYX = 1/2 h (30 + 40)` ...[∵ Area of trapezium = `1/2` sum of parallel sides × distance between them]
= `1/2 h (70)`
= 35 h cm2
Similarly, area of trapezium XYBA
= `1/2 h (40 + 50)`
= `1/2 h xx 90`
= 45 h cm2
∴ `(ar (DCYX))/(ar (XYBA)) = (35h)/(45h) = 7/9`
⇒ `ar (DCYX) = 7/9 ar (XYBA)`
Hence proved.
APPEARS IN
संबंधित प्रश्न
P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
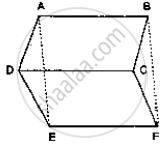
In the given below fig. ABCD, ABFE and CDEF are parallelograms. Prove that ar (ΔADE)
= ar (ΔBCF)
ABCD is a parallelogram, G is the point on AB such that AG = 2 GB, E is a point of DC
such that CE = 2DE and F is the point of BC such that BF = 2FC. Prove that:
(1) ar ( ADEG) = ar (GBCD)
(2) ar (ΔEGB) = `1/6` ar (ABCD)
(3) ar (ΔEFC) = `1/2` ar (ΔEBF)
(4) ar (ΔEBG) = ar (ΔEFC)
(5)ΔFind what portion of the area of parallelogram is the area of EFG.
Two parallelograms are on equal bases and between the same parallels. The ratio of their areas is ______.
PQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm. A is any point on PQ. If PS = 5 cm, then ar (PAS) = 30 cm2.
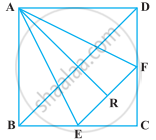
ABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF (Figure), prove that ar (AER) = ar (AFR)
ABCD is a parallelogram in which BC is produced to E such that CE = BC (Figure). AE intersects CD at F. If ar (DFB) = 3 cm2, find the area of the parallelogram ABCD.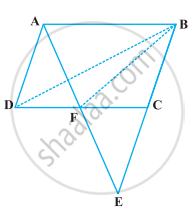
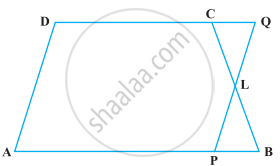
In trapezium ABCD, AB || DC and L is the mid-point of BC. Through L, a line PQ || AD has been drawn which meets AB in P and DC produced in Q (Figure). Prove that ar (ABCD) = ar (APQD)
The diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
In the following figure, ABCD and AEFD are two parallelograms. Prove that ar (PEA) = ar (QFD). [Hint: Join PD].

