Advertisements
Advertisements
प्रश्न
ABCD is a parallelogram, G is the point on AB such that AG = 2 GB, E is a point of DC
such that CE = 2DE and F is the point of BC such that BF = 2FC. Prove that:
(1) ar ( ADEG) = ar (GBCD)
(2) ar (ΔEGB) = `1/6` ar (ABCD)
(3) ar (ΔEFC) = `1/2` ar (ΔEBF)
(4) ar (ΔEBG) = ar (ΔEFC)
(5)ΔFind what portion of the area of parallelogram is the area of EFG.
उत्तर
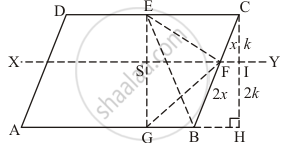
Given,
ABCD is a parallelogram
AG = 2GB,CE = 2DE and BF = 2FC
To prove :
(1) ar (ADEG) = ar (GBCE)
(2) ar (Δ EGB) = `1/6` are (ABCD)
(3) ar (Δ EFC) =`1/2` area (Δ EBF)
(4) area (ΔEBG) = 3/2 area (EFC)
(5) Find what portion of the area of parallelogram is the area of ΔEFG.
Construction: draw EP ⊥ AB and EQ ⊥ BC
Proof : we have,
AG = 2GB and CE = 2DE and BF = 2FC
⇒ AB - GB = 2GB and CD - DE = 2DE and BC - FC
⇒ AB -GB = 2GB and CD - DE = 2DE and BC - FC = 2FC.
⇒ AB =3GB and CD =3DE and BC = 3FC
⇒ `GB = 1/3 AB and DE = `1/3` CD and FC = 1/3 BC ` ............ (1)
(1) ar (ADEG) `1/2` (AG + DE) × EP
⇒ ` ar (ADEG) = 1/2 (2/3AB + 1/3CD) xx EP` [By using(1)]
⇒ `ar (ADEG) = 1/2 (2/3 AB + 1/3 AB)xx EP` [∴ AB = CD]
⇒ `ar (ADEG) = 1/2 xx AB xx EP` ........... (2)
`And ar (GBCE) = 1/2 (GB + CE) xx EP`
⇒ `ar (GBCE) = 1/2 [1/3 AB + 2/3 CD ] xx EP` [By using (1)]
⇒ `ar (GBCE) = 1/2 [1/3 AB + 2/3 AB ] xx EP` [∴ AB = CD]
⇒ `ar (GBCE) = 1/2 xx AB xx EP` ........ (1)
Compare equation (2) and (3)
(2) ar (ΔEGB) = `1/2xx GB xx EP`
= `1/6 xx AB xx EB`
= `1/6 ar (1^(9m) ABCD)`
(3) `Area (ΔEFC) = 1/2 xx FC xx EQ ......... (4)`
`And area (ΔEBF) = 1/2 xx BF xx EQ`
⇒ `ar (ΔEBF) = 1/2 xx2 FC xx EQ ` [BF = 2FC given]
⇒ `ar (ΔEBF) = FC xx EQ` ............. (5)
Compare equation 4 and 5
`Area (ΔEFC) = 1/2 xx area (ΔEBF) `
(4) From (1) part
`ar (ΔEGB ) = 1/6 ar (11^(5m )ABCD)` ....... (6)
Form (3) part
` ar (ΔEFC) =1/2 ar (EBF)`
⇒ `ar (ΔEFC) = 1/3 ar(ΔEBC)`
⇒ `ar (ΔEFC) = 1/3 xx 1/2 xx CE xx EP`
`= 1/2 xx 1/3 xx 2/3 CD xx EP`
`=1/6 xx 2/3 xx ar (11^(gm)ABCD)`
⇒ `ar (ΔEFC) = 2/3 xx ar (ΔEGB)` [By using]
⇒ `ar (ΔEGB) = 3/2 ar (ΔEFC). `
(5) Area (ΔEFG) = ar (Trap . BGEC) = - ar (ΔBGF) → (1)
`Now , area (trap BGEC) = 1/2 (GB + EC) xx EP`
= `1/2 (1/3 AB + 2/3 CD) xx EP `
= `1/2 AB xx EP`
= `1/2 ar (11^(5m)ABCD)`
`Area (ΔEFC) = 1/9 area (11^(5m)ABCD)` [Form 4 part]
And area (Δ BGF) = `1/2 BF xx GR`
`= 1/2 xx 2/3 BC xx GR`
`= 2/3 xx 1/2 BC xx GR `
`= 2/3 xx ar (Δ GBC) `
`= 2/3 xx 1/2 GB xx EP`
`= 1/3 xx 1/3 AB xx EP`
`= 1/9 AB xx EP`
` 1/9 ar ( 11^(gm) ABCD)` [ From (1)]
`ar ( ΔEFG) = 1/2 ar ( 11^(gm) ABCD) = 1/9 ar ( 11^(gm) ABCD) = 1/9 ar ( 11^(gm) ABCD)`
`= 5/18 ar ( 11^(gm) ABCD).`
APPEARS IN
संबंधित प्रश्न
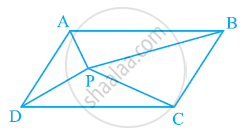
In the given figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar (APB) + ar (PCD) = 1/2ar (ABCD)
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
[Hint: Through. P, draw a line parallel to AB]
Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
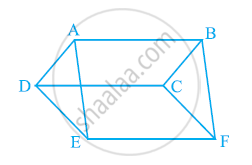
In the following figure, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).
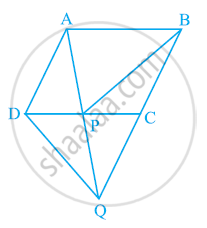
In the following figure, ABCD is parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that
ar (BPC) = ar (DPQ).
[Hint: Join AC.]
In the below fig. ABCD and AEFD are two parallelograms. Prove that
(1) PE = FQ
(2) ar (Δ APE) : ar (ΔPFA) = ar Δ(QFD) : ar (Δ PFD)
(3) ar (ΔPEA) = ar (ΔQFD)
Two parallelograms are on equal bases and between the same parallels. The ratio of their areas is ______.
ABCD is a trapezium with parallel sides AB = a cm and DC = b cm (Figure). E and F are the mid-points of the non-parallel sides. The ratio of ar (ABFE) and ar (EFCD) is ______.
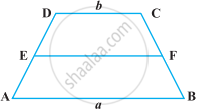
ABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF (Figure), prove that ar (AER) = ar (AFR)
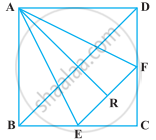
If the mid-points of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram so formed will be half of the area of the given quadrilateral (Figure).
[Hint: Join BD and draw perpendicular from A on BD.]
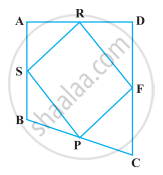
ABCD is a trapezium in which AB || DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that ar (DCYX) = `7/9` ar (XYBA)
