Advertisements
Advertisements
प्रश्न
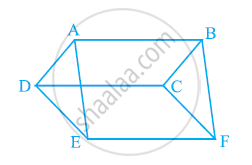
In the following figure, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).
उत्तर
It is given that ABCD is a parallelogram. We know that opposite sides of a parallelogram are equal.
∴ AD = BC ... (1)
Similarly, for parallelograms DCEF and ABFE, it can be proved that
DE = CF ... (2)
And, EA = FB ... (3)
In ΔADE and ΔBCF,
AD = BC ................[Using equation (1)]
DE = CF ................[Using equation (2)]
EA = FB ................[Using equation (3)]
∴ ΔADE ≅ BCF (SSS congruence rule)
⇒ Area (ΔADE) = Area (ΔBCF)
APPEARS IN
संबंधित प्रश्न
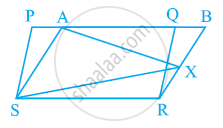
In the given figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = 1/2ar (PQRS)
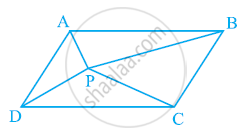
In the given figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar (APB) + ar (PCD) = 1/2ar (ABCD)
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
[Hint: Through. P, draw a line parallel to AB]
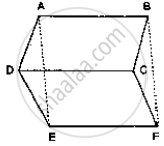
In the given below fig. ABCD, ABFE and CDEF are parallelograms. Prove that ar (ΔADE)
= ar (ΔBCF)
In the below fig. ABCD and AEFD are two parallelograms. Prove that
(1) PE = FQ
(2) ar (Δ APE) : ar (ΔPFA) = ar Δ(QFD) : ar (Δ PFD)
(3) ar (ΔPEA) = ar (ΔQFD)
In which of the following figures, you find two polygons on the same base and between the same parallels?
Two parallelograms are on equal bases and between the same parallels. The ratio of their areas is ______.
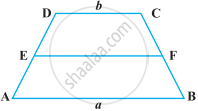
ABCD is a trapezium with parallel sides AB = a cm and DC = b cm (Figure). E and F are the mid-points of the non-parallel sides. The ratio of ar (ABFE) and ar (EFCD) is ______.
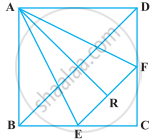
ABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF (Figure), prove that ar (AER) = ar (AFR)
ABCD is a parallelogram in which BC is produced to E such that CE = BC (Figure). AE intersects CD at F. If ar (DFB) = 3 cm2, find the area of the parallelogram ABCD.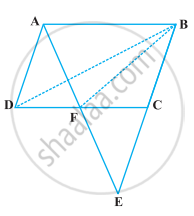
ABCD is a trapezium in which AB || DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that ar (DCYX) = `7/9` ar (XYBA)
