Advertisements
Advertisements
Question
If a triangle and a parallelogram are on the same base and between same parallels, then the ratio of the area of the triangle to the area of parallelogram is ______.
Options
1 : 3
1 : 2
3 : 1
1 : 4
Solution
If a triangle and a parallelogram are on the same base and between same parallels, then the ratio of the area of the triangle to the area of parallelogram is 1 : 2.
Explanation:
We know that, if a parallelogram and a triangle are on the same base and between the same parallels, then area of the triangle is half the area of the parallelogram.
i.e., Area of triangle = `1/2` Area of parallelogram
⇒ `"Area of triangle"/"Area of parallelogram " = 1/2`
∴ Area of triangle : Area of parallelogram = 1 : 2
APPEARS IN
RELATED QUESTIONS
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.
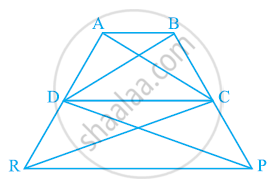
In the given figure, ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
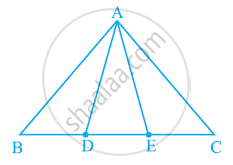
In the following figure, D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) = ar (AEC).
Can you answer the question that you have left in the ’Introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?
[Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide ΔABC into n triangles of equal areas.]
In a ΔABC, if L and M are points on AB and AC respectively such that LM || BC. Prove
that:
(1) ar (ΔLCM ) = ar (ΔLBM )
(2) ar (ΔLBC) = ar (ΔMBC)
(3) ar (ΔABM) ar (ΔACL)
(4) ar (ΔLOB) ar (ΔMOC)
The area of the parallelogram ABCD is 90 cm2 (see figure). Find ar (ΔABD)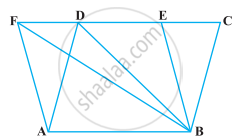
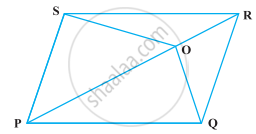
O is any point on the diagonal PR of a parallelogram PQRS (Figure). Prove that ar (PSO) = ar (PQO).
In the following figure, CD || AE and CY || BA. Prove that ar (CBX) = ar (AXY).

If the medians of a ∆ABC intersect at G, show that ar (AGB) = ar (AGC) = ar (BGC) = `1/3` ar (ABC)
