Advertisements
Advertisements
Question
In a ΔABC if D and E are mid-points of BC and AD respectively such that ar (ΔAEC) = 4cm2, then ar (ΔBEC) =
Options
4 cm2
6 cm2
8 cm2
12 cm2
Solution
Given: In ΔABC
(1) D is the midpoint of BC
(2) E is the midpoint of AD
(3) ar (ΔAEC) = 4 cm2
To find: ar (ΔBEC)
Calculation: We know that”the median of the triangle divides the triangle into two triangle of equal area”
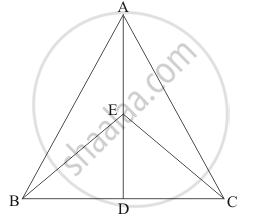
Since AD is the median of ΔABC,
ar (ΔABD) = ar (ΔADC) …… (1)
EC is the median of ΔADC,
ar (ΔAEC) = ar (ΔDEC) …… (2)
⇒ ar (ΔDEC) = 4 cm2
EC is the median of ΔBED
ar (ΔBED) = ar (ΔDEC) …… (3)
From 2 and 3 we get,
ar (ΔBED) = ar (ΔAEC) …… (4)
⇒ ar (ΔBED) = 4 cm2
Now,
ar (ΔBEC) = ar (ΔBED) + ar (ΔDEC)
= 4 + 4 (subsituting the values)
ar(ΔBEC) = 8 cm2
APPEARS IN
RELATED QUESTIONS
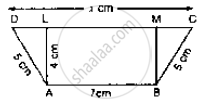
In the below fig. ABCD is a trapezium in which AB = 7 cm, AD = BC = 5 cm, DC = x cm,
and distance between AB and DC is 4cm. Find the value of x and area of trapezium ABCD.
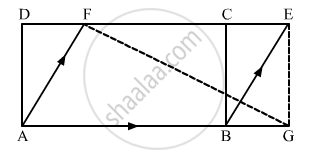
In the given figure, ABCD is a rectangle with sides AB = 10 cm and AD = 5 cm. Find the area of ΔEFG.
P is any point on base BC of ΔABC and D is the mid-point of BC. DE is drawn parallel toPA to meet AC at E. If ar (ΔABC) = 12 cm2, then find area of ΔEPC.
The figure obtained by joining the mid-points of the adjacent sides of a rectangle of sides 8 cm and 6 cm is ______.
If AD is median of ΔABC and P is a point on AC such that
ar (ΔADP) : ar (ΔABD) = 2 : 3, then ar (Δ PDC) : ar (Δ ABC)
Find the area of a rectangle whose length = 24 cm breadth =180 mm
What will happen to the area of a rectangle, if its length and breadth both are trebled?
Is the area of both your footprints the same?
Find the area of the following figure by counting squares:

Find the area of the following figure by counting squares:

