Advertisements
Advertisements
प्रश्न
In a ΔABC if D and E are mid-points of BC and AD respectively such that ar (ΔAEC) = 4cm2, then ar (ΔBEC) =
विकल्प
4 cm2
6 cm2
8 cm2
12 cm2
उत्तर
Given: In ΔABC
(1) D is the midpoint of BC
(2) E is the midpoint of AD
(3) ar (ΔAEC) = 4 cm2
To find: ar (ΔBEC)
Calculation: We know that”the median of the triangle divides the triangle into two triangle of equal area”
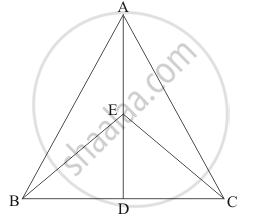
Since AD is the median of ΔABC,
ar (ΔABD) = ar (ΔADC) …… (1)
EC is the median of ΔADC,
ar (ΔAEC) = ar (ΔDEC) …… (2)
⇒ ar (ΔDEC) = 4 cm2
EC is the median of ΔBED
ar (ΔBED) = ar (ΔDEC) …… (3)
From 2 and 3 we get,
ar (ΔBED) = ar (ΔAEC) …… (4)
⇒ ar (ΔBED) = 4 cm2
Now,
ar (ΔBEC) = ar (ΔBED) + ar (ΔDEC)
= 4 + 4 (subsituting the values)
ar(ΔBEC) = 8 cm2
APPEARS IN
संबंधित प्रश्न
ABCD is a parallelogram whose diagonals AC and BD intersect at O. A line through O
intersects AB at P and DC at Q. Prove that ar (Δ POA) = ar (Δ QOC).
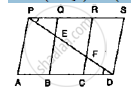
In below fig., PSDA is a parallelogram in which PQ = QR = RS and AP || BQ || CR. Prove
that ar (Δ PQE) = ar (ΔCFD).
ABCD is a parallelogram. P is the mid-point of AB. BD and CP intersect at Q such that CQ: QP = 3.1. If ar (ΔPBQ) = 10cm2, find the area of parallelogram ABCD.
In a ΔABC, D, E, F are the mid-points of sides BC, CA and AB respectively. If ar (ΔABC) = 16cm2, then ar (trapezium FBCE) =
ABCD is a trapezium with parallel sides AB =a and DC = b. If E and F are mid-points of non-parallel sides AD and BC respectively, then the ratio of areas of quadrilaterals ABFEand EFCD is
Find the area of a square, whose side is: 4.5 cm.
By counting squares, estimate the area of the figure.

Is the area of both your footprints the same?
Find the area of the following figure by counting squares:

Find the area of the following figure by counting squares:

