Advertisements
Advertisements
Question
What will happen to the area of a rectangle, if its length and breadth both are trebled?
Solution
Let the original length of the rectangle = l and its original breadth = b
∴ its original area = length x breadth i.e A = l – b i. e.
Since,
Increased length -=3l
and, increased breadth = 3b
∴ New area = 3l x 3b = 9 x l x b [∵A = l x b]
⇒ Area of the new rectangle = 9 times than area of original rectangle
APPEARS IN
RELATED QUESTIONS
In Q. No 1, if AD = 6 cm, CF = 10 cm, and AE = 8cm, find AB.
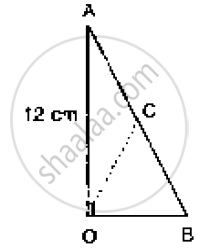
In the below fig. ∠AOB = 90°, AC = BC, OA = 12 cm and OC = 6.5 cm. Find the area of
ΔAOB.
If P is any point in the interior of a parallelogram ABCD, then prove that area of the
triangle APB is less than half the area of parallelogram.
ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects
CD at F.
(i) Prove that ar (ΔADF) = ar (ΔECF)
(ii) If the area of ΔDFB = 3 cm2, find the area of ||gm ABCD.
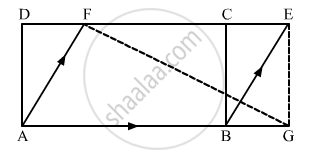
In the given figure, ABCD is a rectangle with sides AB = 10 cm and AD = 5 cm. Find the area of ΔEFG.
P is any point on base BC of ΔABC and D is the mid-point of BC. DE is drawn parallel toPA to meet AC at E. If ar (ΔABC) = 12 cm2, then find area of ΔEPC.
A triangle and a parallelogram are on the same base and between the same parallels. The ratio of the areas of triangle and parallelogram is
In a ΔABC, D, E, F are the mid-points of sides BC, CA and AB respectively. If ar (ΔABC) = 16cm2, then ar (trapezium FBCE) =
The medians of a triangle ABC intersect each other at point G. If one of its medians is AD,
prove that:
(i) Area ( ΔABD ) = 3 x Area ( ΔBGD )
(ii) Area ( ΔACD ) = 3 x Area ( ΔCGD )
(iii) Area ( ΔBGC ) = `1/3` x Area ( ΔABC ).
Look at a 10 rupee note. Is its area more than hundred square cm?
