Advertisements
Advertisements
Question
The medians of a triangle ABC intersect each other at point G. If one of its medians is AD,
prove that:
(i) Area ( ΔABD ) = 3 x Area ( ΔBGD )
(ii) Area ( ΔACD ) = 3 x Area ( ΔCGD )
(iii) Area ( ΔBGC ) = `1/3` x Area ( ΔABC ).
Solution
(i) The figure is shown below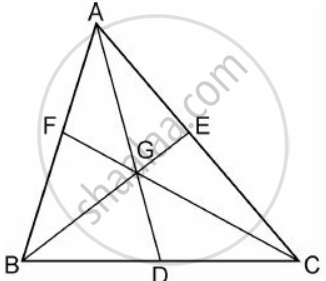
(i) Medians intersect at centroid.
Given that C is the point of intersection of medians and hence G is the centroid of the triangle ABC.
Centroid divides the medians in the ratio 2: 1
That is AG: GD = 2: 1.
Since BG divides AD in the ratio 2: 1, we have,
`"A( ΔAGB )"/"A( ΔBGD)" = 2/1`
⇒ Area( ΔAGB ) = 2Area( ΔBGD )
From the figure, it is clear that,
Area( ΔABD ) = Area( ΔAGB ) + Area( ΔBGD )
⇒ Area( ΔABD ) = 2Area( ΔBGD ) + Area( ΔBGD )
⇒ Area( ΔABD ) = 3Area( ΔBGD ) ......(1)
(ii) Medians intersect at centroid.
Given that G is the point of intersection of medians and hence G is the centroid of the triangle ABC.
Centroid divides the medians in the ratio 2: 1
That is AG: GD = 2: 1.
Since CG divides AD in the ratio 2: 1, we have,
`"A( ΔAGC )"/"A( ΔCGD)" = 2/1`
⇒ Area( ΔAGC ) = 2Area( ΔCGD )
From the figure, it is clear that,
Area( ΔACD ) = Area( ΔAGC ) + Area( ΔCGD )
⇒ Area( ΔACD ) = 2Area( ΔCGD ) + Area( ΔCGD )
⇒ Area( ΔACD ) = 3Area( ΔCGD ) ......(2)
(iii) Adding equations (1) and (2), We have,
Area( ΔABD ) + Area( ΔACD ) = 3Area( ΔBGD ) + 3Area( ΔCGD )
⇒ Area( ΔABC ) = 3[ Area( ΔBGD ) + Area( ΔCGD ) ]
⇒ Area( ΔABC ) = 3[ Area( ΔBGC ) ]
⇒ `"Area( ΔABC )"/3 = [ Area( ΔBGC )]`
⇒ Area( ΔBGC ) = `1/3` Area( ΔABC )
APPEARS IN
RELATED QUESTIONS
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that:
ar(ΔAPB) × ar(ΔCPD) = ar(ΔAPD) × ar (ΔBPC)
In the below Fig, ABC and ABD are two triangles on the base AB. If line segment CD is
bisected by AB at O, show that ar (Δ ABC) = ar (Δ ABD)

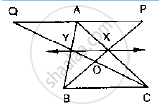
In the below fig. X and Y are the mid-points of AC and AB respectively, QP || BC and
CYQ and BXP are straight lines. Prove that ar (Δ ABP) = ar (ΔACQ).
ABCD is a rectangle with O as any point in its interior. If ar (ΔAOD) = 3 cm2 and ar (ΔABOC) = 6 cm2, then area of rectangle ABCD is
The length and breadth of a rectangular piece of land are in the ratio 5 : 3. If the total cost of fencing it at the rate of ₹24 per meter is ₹9600, find its :
(i) length and breadth
(ii) area
(iii) cost of levelling at the rate of ₹60 per m2.
Length of a rectangle is 30 m and its breadth is 20 m. Find the increase in its area if its length is increased by 10 m and its breadth is doubled.
Measure the length of the floor of your classroom in meters. Also, measure the width.
- So how many children can sit in one square meter?
The region given in the following figure is measured by taking  as a unit. What is the area of the region?
as a unit. What is the area of the region?
How will you decide? Discuss.
Find the area of the following figure by counting squares:

