Advertisements
Advertisements
प्रश्न
The medians of a triangle ABC intersect each other at point G. If one of its medians is AD,
prove that:
(i) Area ( ΔABD ) = 3 x Area ( ΔBGD )
(ii) Area ( ΔACD ) = 3 x Area ( ΔCGD )
(iii) Area ( ΔBGC ) = `1/3` x Area ( ΔABC ).
उत्तर
(i) The figure is shown below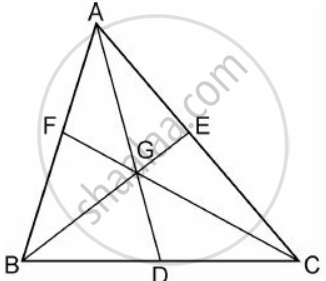
(i) Medians intersect at centroid.
Given that C is the point of intersection of medians and hence G is the centroid of the triangle ABC.
Centroid divides the medians in the ratio 2: 1
That is AG: GD = 2: 1.
Since BG divides AD in the ratio 2: 1, we have,
`"A( ΔAGB )"/"A( ΔBGD)" = 2/1`
⇒ Area( ΔAGB ) = 2Area( ΔBGD )
From the figure, it is clear that,
Area( ΔABD ) = Area( ΔAGB ) + Area( ΔBGD )
⇒ Area( ΔABD ) = 2Area( ΔBGD ) + Area( ΔBGD )
⇒ Area( ΔABD ) = 3Area( ΔBGD ) ......(1)
(ii) Medians intersect at centroid.
Given that G is the point of intersection of medians and hence G is the centroid of the triangle ABC.
Centroid divides the medians in the ratio 2: 1
That is AG: GD = 2: 1.
Since CG divides AD in the ratio 2: 1, we have,
`"A( ΔAGC )"/"A( ΔCGD)" = 2/1`
⇒ Area( ΔAGC ) = 2Area( ΔCGD )
From the figure, it is clear that,
Area( ΔACD ) = Area( ΔAGC ) + Area( ΔCGD )
⇒ Area( ΔACD ) = 2Area( ΔCGD ) + Area( ΔCGD )
⇒ Area( ΔACD ) = 3Area( ΔCGD ) ......(2)
(iii) Adding equations (1) and (2), We have,
Area( ΔABD ) + Area( ΔACD ) = 3Area( ΔBGD ) + 3Area( ΔCGD )
⇒ Area( ΔABC ) = 3[ Area( ΔBGD ) + Area( ΔCGD ) ]
⇒ Area( ΔABC ) = 3[ Area( ΔBGC ) ]
⇒ `"Area( ΔABC )"/3 = [ Area( ΔBGC )]`
⇒ Area( ΔBGC ) = `1/3` Area( ΔABC )
APPEARS IN
संबंधित प्रश्न
Let ABCD be a parallelogram of area 124 cm2. If E and F are the mid-points of sides AB and
CD respectively, then find the area of parallelogram AEFD.
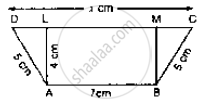
In the below fig. ABCD is a trapezium in which AB = 7 cm, AD = BC = 5 cm, DC = x cm,
and distance between AB and DC is 4cm. Find the value of x and area of trapezium ABCD.
ABCD is a parallelogram. E is a point on BA such that BE = 2 EA and F is a point on DC
such that DF = 2 FC. Prove that AE CF is a parallelogram whose area is one third of the
area of parallelogram ABCD.
A triangle and a parallelogram are on the same base and between the same parallels. The ratio of the areas of triangle and parallelogram is
ABCD is a rectangle with O as any point in its interior. If ar (ΔAOD) = 3 cm2 and ar (ΔABOC) = 6 cm2, then area of rectangle ABCD is
The table given below contains some measures of the rectangle. Find the unknown values.
| Length | Breadth | Perimeter | Area |
| ? | 15 cm | 60 cm | ? |
Each line gives a story. You have to choose the question which makes the best story problem. The first one is already marked.
- 352 children from a school went on a camping trip. Each tent had a group of 4 children.
a) How many children did each tent have? b) How many tents do they need? c) How many children in all are in the school?
In the following figure, the area of parallelogram ABCD is ______.
Area of a rectangle with length 5 cm and breadth 3 cm is ______.
Find the area of the following figure by counting squares:

