Advertisements
Chapters
2: Compound Interest (Without using formula)
3: Compound Interest (Using Formula)
4: Expansions (Including Substitution)
5: Factorisation
6: Simultaneous (Linear) Equations (Including Problems)
7: Indices (Exponents)
8: Logarithms
9: Triangles [Congruency in Triangles]
10: Isosceles Triangles
11: Inequalities
12: Mid-point and Its Converse [ Including Intercept Theorem]
13: Pythagoras Theorem [Proof and Simple Applications with Converse]
14: Rectilinear Figures [Quadrilaterals: Parallelogram, Rectangle, Rhombus, Square and Trapezium]
15: Construction of Polygons (Using ruler and compass only)
▶ 16: Area Theorems [Proof and Use]
17: Circle
18: Statistics
19: Mean and Median (For Ungrouped Data Only)
20: Area and Perimeter of Plane Figures
21: Solids [Surface Area and Volume of 3-D Solids]
22: Trigonometrical Ratios [Sine, Consine, Tangent of an Angle and their Reciprocals]
23: Trigonometrical Ratios of Standard Angles [Including Evaluation of an Expression Involving Trigonometric Ratios]
24: Solution of Right Triangles [Simple 2-D Problems Involving One Right-angled Triangle]
25: Complementary Angles
26: Co-ordinate Geometry
27: Graphical Solution (Solution of Simultaneous Linear Equations, Graphically)
28: Distance Formula
![Selina solutions for Concise Mathematics [English] Class 9 ICSE chapter 16 - Area Theorems [Proof and Use] Selina solutions for Concise Mathematics [English] Class 9 ICSE chapter 16 - Area Theorems [Proof and Use] - Shaalaa.com](/images/concise-mathematics-english-class-9-icse_6:b313c06da7fb4b0f885a06c3b5e4e4fa.jpg)
Advertisements
Solutions for Chapter 16: Area Theorems [Proof and Use]
Below listed, you can find solutions for Chapter 16 of CISCE Selina for Concise Mathematics [English] Class 9 ICSE.
Selina solutions for Concise Mathematics [English] Class 9 ICSE 16 Area Theorems [Proof and Use] Exercise 16 (A) [Pages 196 - 198]
In the given figure, if the area of triangle ADE is 60 cm2, state, given reason, the area of :
(i) Parallelogram ABED;
(ii) Rectangle ABCF;
(iii) Triangle ABE.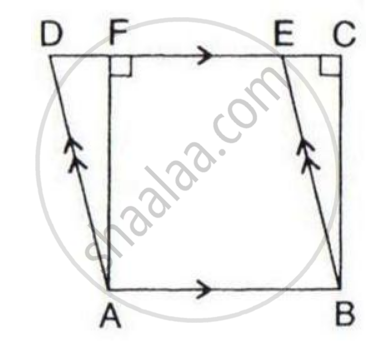
The given figure shows a rectangle ABDC and a parallelogram ABEF; drawn on opposite sides of AB.
Prove that:
(i) Quadrilateral CDEF is a parallelogram;
(ii) Area of the quad. CDEF
= Area of rect. ABDC + Area of // gm. ABEF.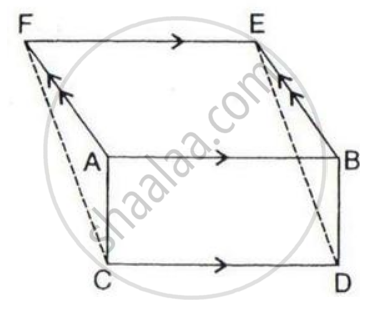
In the given figure, diagonals PR and QS of the parallelogram PQRS intersect at point O and LM is parallel to PS. Show that: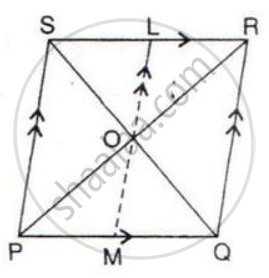
(i) 2 Area (POS) = Area (// gm PMLS)
(ii) Area (POS) + Area (QOR) = Area (// gm PQRS)
(iii) Area (POS) + Area (QOR) = Area (POQ) + Area (SOR).
In parallelogram ABCD, P is a point on side AB and Q is a point on side BC.
Prove that:
(i) ΔCPD and ΔAQD are equal in the area.
(ii) Area (ΔAQD) = Area (ΔAPD) + Area (ΔCPB)
In the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD.
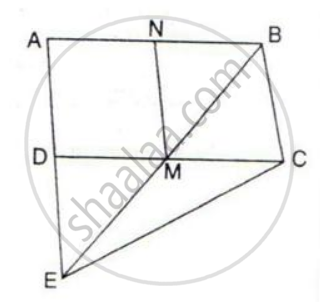
If the area of parallelogram ABCD is 48 cm2;
(i) State the area of the triangle BEC.
(ii) Name the parallelogram which is equal in area to the triangle BEC.
In the following figure, CE is drawn parallel to diagonals DB of the quadrilateral ABCD which meets AB produced at point E.
Prove that ΔADE and quadrilateral ABCD are equal in area.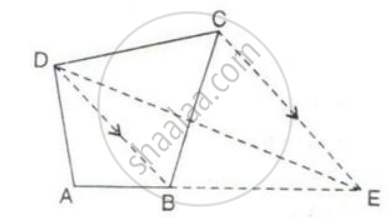
ABCD is a parallelogram a line through A cuts DC at point P and BC produced at Q. Prove that triangle BCP is equal in area to triangle DPQ.
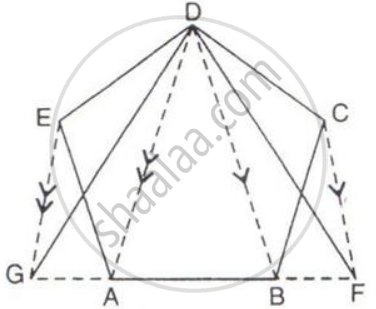
The given figure shows a pentagon ABCDE. EG drawn parallel to DA meets BA produced at G and CF draw parallel to DB meets AB produced at F.
Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.
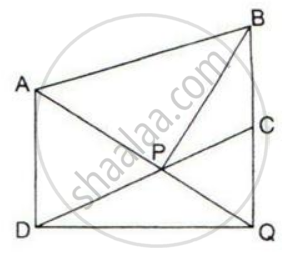
In the given figure, AP is parallel to BC, BP is parallel to CQ.
Prove that the area of triangles ABC and BQP are equal.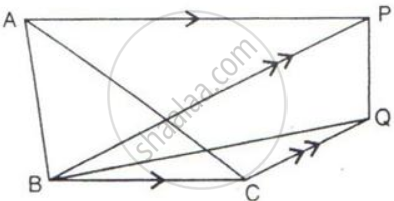
In the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC.
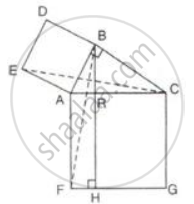
If BH is perpendicular to FG
prove that:
- ΔEAC ≅ ΔBAF
- Area of the square ABDE
- Area of the rectangle ARHF.
In the following figure, DE is parallel to BC.
Show that:
(i) Area ( ΔADC ) = Area( ΔAEB ).
(ii) Area ( ΔBOD ) = Area( ΔCOE ).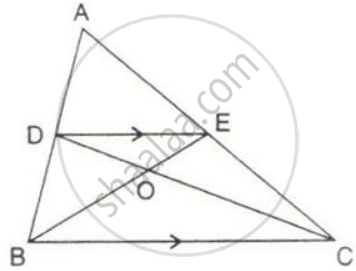
ABCD and BCFE are parallelograms. If area of triangle EBC = 480 cm2; AB = 30 cm and BC = 40 cm.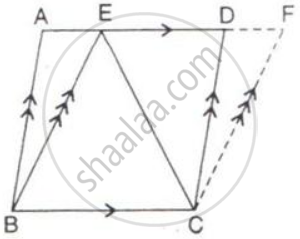
Calculate :
(i) Area of parallelogram ABCD;
(ii) Area of the parallelogram BCFE;
(iii) Length of altitude from A on CD;
(iv) Area of triangle ECF.
In the given figure, D is mid-point of side AB of ΔABC and BDEC is a parallelogram.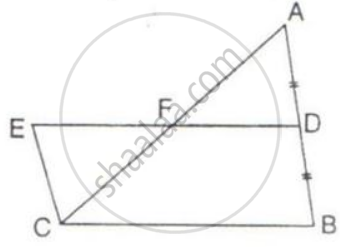
Prove that: Area of ABC = Area of // gm BDEC.
In the following, AC // PS // QR and PQ // DB // SR.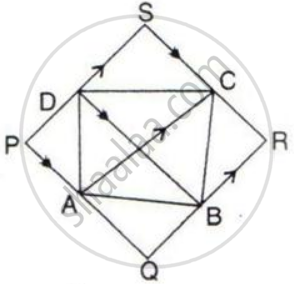
Prove that: Area of quadrilateral PQRS = 2 x Area of the quad. ABCD.
ABCD is a trapezium with AB // DC. A line parallel to AC intersects AB at point M and BC at point N.
Prove that: area of Δ ADM = area of Δ ACN.
In the given figure, AD // BE // CF.
Prove that area (ΔAEC) = area (ΔDBF)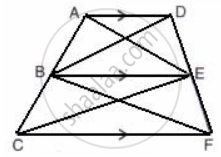
In the given figure, ABCD is a parallelogram; BC is produced to point X.
Prove that: area ( Δ ABX ) = area (`square`ACXD )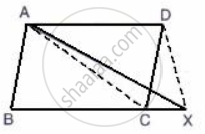
The given figure shows the parallelograms ABCD and APQR.
Show that these parallelograms are equal in the area.
[ Join B and R ]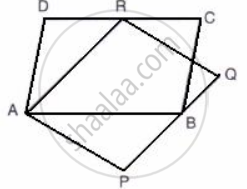
Selina solutions for Concise Mathematics [English] Class 9 ICSE 16 Area Theorems [Proof and Use] Exercise 16 (B) [Page 201]
Show that:
A diagonal divides a parallelogram into two triangles of equal area.
Show that:
The ratio of the areas of two triangles of the same height is equal to the ratio of their bases.
Show that:
The ratio of the areas of two triangles on the same base is equal to the ratio of their heights.
In the given figure; AD is median of ΔABC and E is any point on median AD.
Prove that Area (ΔABE) = Area (ΔACE).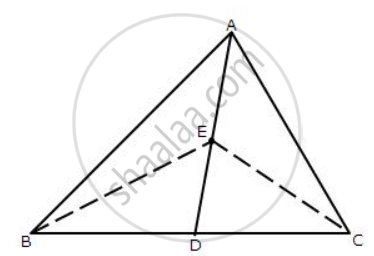
In the figure of question 2, if E is the mid-point of median AD, then
prove that:
Area (ΔABE) = `1/4` Area (ΔABC).
ABCD is a parallelogram. P and Q are the mid-points of sides AB and AD respectively.
Prove that area of triangle APQ = `1/8` of the area of parallelogram ABCD.
The base BC of triangle ABC is divided at D so that BD = `1/2`DC.
Prove that area of ΔABD = `1/3` of the area of ΔABC.
In a parallelogram ABCD, point P lies in DC such that DP: PC = 3:2. If the area of ΔDPB = 30 sq. cm.
find the area of the parallelogram ABCD.
ABCD is a parallelogram in which BC is produced to E such that CE = BC and AE intersects CD at F.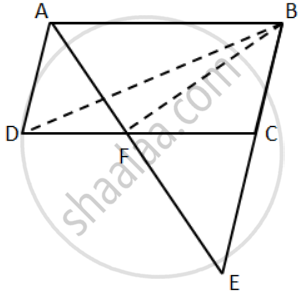
If ar.(∆DFB) = 30 cm2; find the area of parallelogram.
The following figure shows a triangle ABC in which P, Q, and R are mid-points of sides AB, BC and CA respectively. S is mid-point of PQ:
Prove that: ar. ( ∆ ABC ) = 8 × ar. ( ∆ QSB )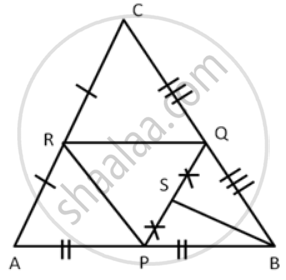
Selina solutions for Concise Mathematics [English] Class 9 ICSE 16 Area Theorems [Proof and Use] Exercise 16 (C) [Pages 201 - 202]
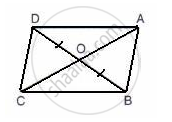
In the given figure, the diagonals AC and BD intersect at point O. If OB = OD and AB//DC,
show that:
(i) Area (Δ DOC) = Area (Δ AOB).
(ii) Area (Δ DCB) = Area (Δ ACB).
(iii) ABCD is a parallelogram.
The given figure shows a parallelogram ABCD with area 324 sq. cm. P is a point in AB such that AP: PB = 1:2
Find The area of Δ APD.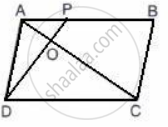
In ΔABC, E and F are mid-points of sides AB and AC respectively. If BF and CE intersect each other at point O,
prove that the ΔOBC and quadrilateral AEOF are equal in area.
In parallelogram ABCD, P is the mid-point of AB. CP and BD intersect each other at point O. If the area of ΔPOB = 40 cm2, and OP: OC = 1:2, find:
(i) Areas of ΔBOC and ΔPBC
(ii) Areas of ΔABC and parallelogram ABCD.
The medians of a triangle ABC intersect each other at point G. If one of its medians is AD,
prove that:
(i) Area ( ΔABD ) = 3 x Area ( ΔBGD )
(ii) Area ( ΔACD ) = 3 x Area ( ΔCGD )
(iii) Area ( ΔBGC ) = `1/3` x Area ( ΔABC ).
The perimeter of a triangle ABC is 37 cm and the ratio between the lengths of its altitudes be 6: 5: 4. Find the lengths of its sides.
Let the sides be x cm, y cm, and (37 - x - y) cm. Also, let the lengths of altitudes be 6a cm, 5a cm, and 4a cm.
In parallelogram ABCD, E is a point in AB and DE meets diagonal AC at point F. If DF: FE = 5:3 and area of ΔADF is 60 cm2; find
(i) area of ΔADE.
(ii) if AE: EB = 4:5, find the area of ΔADB.
(iii) also, find the area of parallelogram ABCD.
In the following figure, BD is parallel to CA, E is mid-point of CA and BD = `1/2`CA
Prove that: ar. ( ΔABC ) = 2 x ar.( ΔDBC )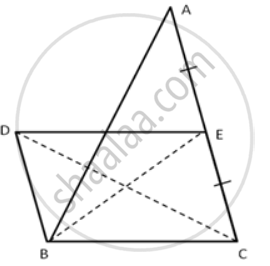
In the following figure, OAB is a triangle and AB || DC.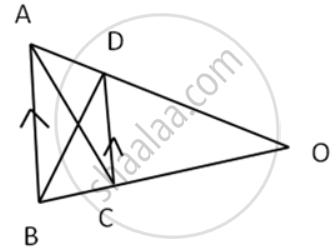
If the area of ∆ CAD = 140 cm2 and the area of ∆ ODC = 172 cm2,
find : (i) the area of ∆ DBC
(ii) the area of ∆ OAC
(iii) the area of ∆ ODB.
E, F, G, and H are the midpoints of the sides of a parallelogram ABCD.
Show that the area of quadrilateral EFGH is half of the area of parallelogram ABCD.
ABCD is a trapezium with AB parallel to DC. A line parallel to AC intersects AB at X and BC at Y.
Prove that the area of ∆ADX = area of ∆ACY.
Solutions for 16: Area Theorems [Proof and Use]
![Selina solutions for Concise Mathematics [English] Class 9 ICSE chapter 16 - Area Theorems [Proof and Use] Selina solutions for Concise Mathematics [English] Class 9 ICSE chapter 16 - Area Theorems [Proof and Use] - Shaalaa.com](/images/concise-mathematics-english-class-9-icse_6:b313c06da7fb4b0f885a06c3b5e4e4fa.jpg)
Selina solutions for Concise Mathematics [English] Class 9 ICSE chapter 16 - Area Theorems [Proof and Use]
Shaalaa.com has the CISCE Mathematics Concise Mathematics [English] Class 9 ICSE CISCE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Selina solutions for Mathematics Concise Mathematics [English] Class 9 ICSE CISCE 16 (Area Theorems [Proof and Use]) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Selina textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Concise Mathematics [English] Class 9 ICSE chapter 16 Area Theorems [Proof and Use] are Figures Between the Same Parallels, Triangles with the Same Vertex and Bases Along the Same Line, Concept of Area.
Using Selina Concise Mathematics [English] Class 9 ICSE solutions Area Theorems [Proof and Use] exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Selina Solutions are essential questions that can be asked in the final exam. Maximum CISCE Concise Mathematics [English] Class 9 ICSE students prefer Selina Textbook Solutions to score more in exams.
Get the free view of Chapter 16, Area Theorems [Proof and Use] Concise Mathematics [English] Class 9 ICSE additional questions for Mathematics Concise Mathematics [English] Class 9 ICSE CISCE, and you can use Shaalaa.com to keep it handy for your exam preparation.
