Advertisements
Advertisements
Question
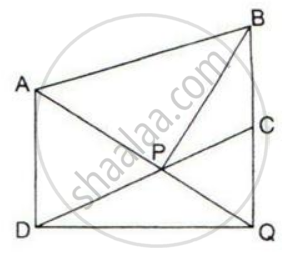
ABCD is a parallelogram a line through A cuts DC at point P and BC produced at Q. Prove that triangle BCP is equal in area to triangle DPQ.
Solution
ΔAPB and parallelogram ABCD are on the same base AB and between the same parallel lines AB and CD.
∴ Ar. ( ΔAPB ) = `1/2` Ar.( parallelogram ABCD ) ......(i)
ΔADQ and parallelogram ABCD are on the same base AD and between the same parallel lines AD and BQ.
∴ Ar.( ΔADQ ) = `1/2` Ar.( parallelogram ABCD ) ......(ii)
Adding equation (i) and (ii), we get
∴ Ar.( ΔAPB ) + Ar.( ΔADQ ) = Ar.(parallelogram ABCD)
Ar.( quad ADQB ) - Ar.(Δ BPQ ) = Ar.(parallelogram ABCD)
Ar.( quad ADQB) - Ar.( ΔBPQ ) = Ar.(quad ADQB ) -Ar.( ΔDCQ )
Ar. ( ΔBPQ ) = Ar. ( ΔDCQ )
Subtracting Ar.ΔPCQ from both sides, we get
Ar. ( ΔBPQ ) - Ar.(ΔPCQ ) = Ar. ( ΔDCQ ) - Ar. ( ΔPCQ)
Ar. ( ΔBCP ) = Ar. ( ΔDPQ )
Hence proved.
APPEARS IN
RELATED QUESTIONS
The given figure shows the parallelograms ABCD and APQR.
Show that these parallelograms are equal in the area.
[ Join B and R ]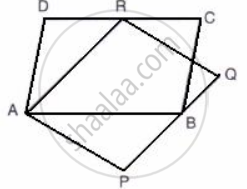
The given figure shows a rectangle ABDC and a parallelogram ABEF; drawn on opposite sides of AB.
Prove that:
(i) Quadrilateral CDEF is a parallelogram;
(ii) Area of the quad. CDEF
= Area of rect. ABDC + Area of // gm. ABEF.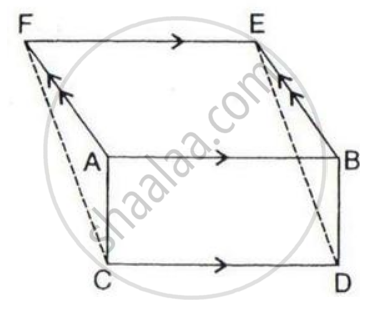
In the given figure, AD // BE // CF.
Prove that area (ΔAEC) = area (ΔDBF)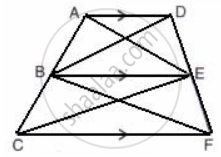
In the given figure, diagonals PR and QS of the parallelogram PQRS intersect at point O and LM is parallel to PS. Show that: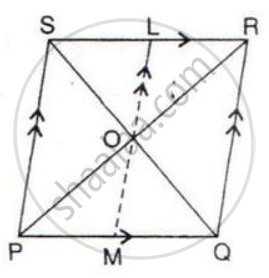
(i) 2 Area (POS) = Area (// gm PMLS)
(ii) Area (POS) + Area (QOR) = Area (// gm PQRS)
(iii) Area (POS) + Area (QOR) = Area (POQ) + Area (SOR).
In parallelogram ABCD, P is a point on side AB and Q is a point on side BC.
Prove that:
(i) ΔCPD and ΔAQD are equal in the area.
(ii) Area (ΔAQD) = Area (ΔAPD) + Area (ΔCPB)
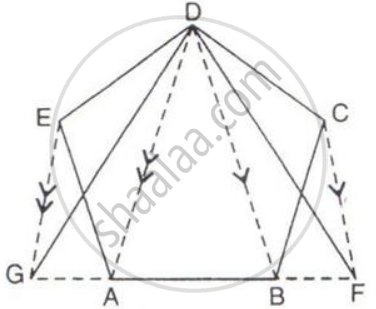
The given figure shows a pentagon ABCDE. EG drawn parallel to DA meets BA produced at G and CF draw parallel to DB meets AB produced at F.
Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.
Show that:
A diagonal divides a parallelogram into two triangles of equal area.
ABCD is a parallelogram in which BC is produced to E such that CE = BC and AE intersects CD at F.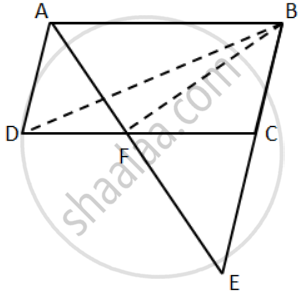
If ar.(∆DFB) = 30 cm2; find the area of parallelogram.
The given figure shows a parallelogram ABCD with area 324 sq. cm. P is a point in AB such that AP: PB = 1:2
Find The area of Δ APD.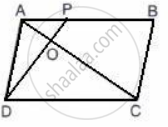
Show that:
The ratio of the areas of two triangles of the same height is equal to the ratio of their bases.
