Advertisements
Advertisements
Question
In the following figure, CE is drawn parallel to diagonals DB of the quadrilateral ABCD which meets AB produced at point E.
Prove that ΔADE and quadrilateral ABCD are equal in area.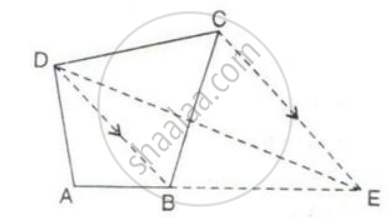
Solution
Since ΔDCB and ΔDEB are on the same base DB and between the same parallels i.e. DB // CE, therefore we get
Ar. ( ΔDCB) = Ar. ( ΔDEB )
Ar. ( ΔDCB + ΔADB ) = AR. (ΔDEB + ΔADB )
Ar. ( ABCD ) = Ar. ( ΔADE )
Hence proved.
APPEARS IN
RELATED QUESTIONS
In the given figure, if the area of triangle ADE is 60 cm2, state, given reason, the area of :
(i) Parallelogram ABED;
(ii) Rectangle ABCF;
(iii) Triangle ABE.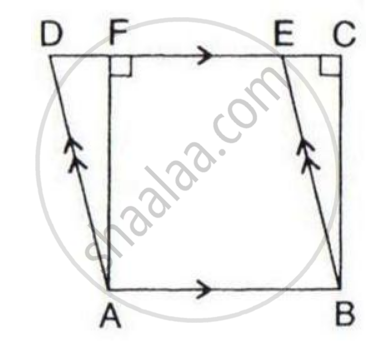
In the given figure, ABCD is a parallelogram; BC is produced to point X.
Prove that: area ( Δ ABX ) = area (`square`ACXD )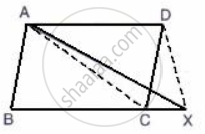
ABCD and BCFE are parallelograms. If area of triangle EBC = 480 cm2; AB = 30 cm and BC = 40 cm.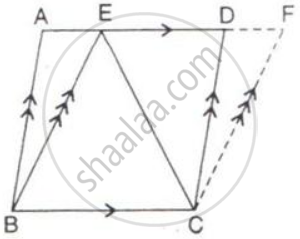
Calculate :
(i) Area of parallelogram ABCD;
(ii) Area of the parallelogram BCFE;
(iii) Length of altitude from A on CD;
(iv) Area of triangle ECF.
In the following figure, DE is parallel to BC.
Show that:
(i) Area ( ΔADC ) = Area( ΔAEB ).
(ii) Area ( ΔBOD ) = Area( ΔCOE ).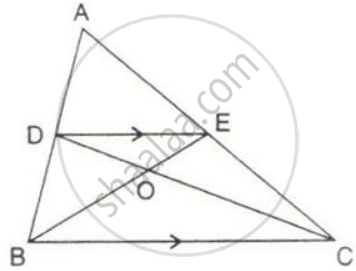
In the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD.
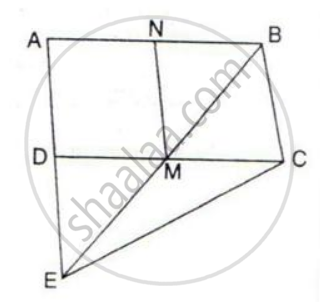
If the area of parallelogram ABCD is 48 cm2;
(i) State the area of the triangle BEC.
(ii) Name the parallelogram which is equal in area to the triangle BEC.
ABCD is a parallelogram. P and Q are the mid-points of sides AB and AD respectively.
Prove that area of triangle APQ = `1/8` of the area of parallelogram ABCD.
ABCD is a trapezium with AB parallel to DC. A line parallel to AC intersects AB at X and BC at Y.
Prove that the area of ∆ADX = area of ∆ACY.
E, F, G, and H are the midpoints of the sides of a parallelogram ABCD.
Show that the area of quadrilateral EFGH is half of the area of parallelogram ABCD.
In the following figure, BD is parallel to CA, E is mid-point of CA and BD = `1/2`CA
Prove that: ar. ( ΔABC ) = 2 x ar.( ΔDBC )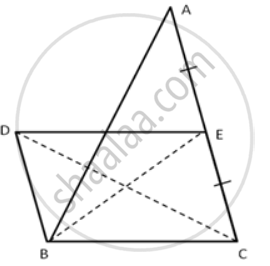
In parallelogram ABCD, E is a point in AB and DE meets diagonal AC at point F. If DF: FE = 5:3 and area of ΔADF is 60 cm2; find
(i) area of ΔADE.
(ii) if AE: EB = 4:5, find the area of ΔADB.
(iii) also, find the area of parallelogram ABCD.
