Advertisements
Advertisements
Question
In parallelogram ABCD, E is a point in AB and DE meets diagonal AC at point F. If DF: FE = 5:3 and area of ΔADF is 60 cm2; find
(i) area of ΔADE.
(ii) if AE: EB = 4:5, find the area of ΔADB.
(iii) also, find the area of parallelogram ABCD.
Solution
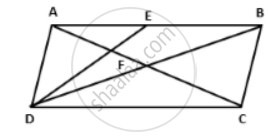
ΔADF and ΔAFE have the same vertex A and their bases are on the same straight line DE.
∴ `"A(ΔADF)"/"A(ΔAFE)" = "DF"/"FE"`
⇒ `60/"A(ΔAFE)" = 5/3 `
⇒ A(ΔAFE) = `( 60 xx 3 )/5` = 36cm2.
Now, A(ΔADE) = A(ΔADF) + A(ΔAFE) = 60 + 36 = 96 cm2.
ΔADE and ΔEDB have the same vertex D and their bases are on the same straight line AB.\
∴ `"A( ΔADE )"/"A( ΔEDB )" = "AE"/"EB"`
⇒ `96/"A( ΔEDB )" = 4/5`
⇒ A( ΔEDB ) = `( 96 xx 5 )/4` = 120 cm2 .
Now, A( ΔADB ) and ||m ABCD are on the same base AB and between the same parallels AB and DC.
∴ A( ΔADB ) = `1/2` A( ||m ABCD )
⇒ 216 = `1/2` A( ||m ABCD )
⇒ A( ||m ABCD ) = 2 x 216 = 432 cm2 .
APPEARS IN
RELATED QUESTIONS
The given figure shows the parallelograms ABCD and APQR.
Show that these parallelograms are equal in the area.
[ Join B and R ]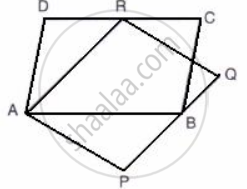
The given figure shows a rectangle ABDC and a parallelogram ABEF; drawn on opposite sides of AB.
Prove that:
(i) Quadrilateral CDEF is a parallelogram;
(ii) Area of the quad. CDEF
= Area of rect. ABDC + Area of // gm. ABEF.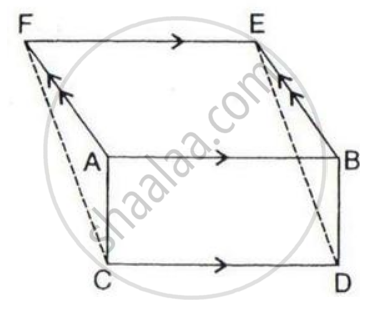
In the given figure, AD // BE // CF.
Prove that area (ΔAEC) = area (ΔDBF)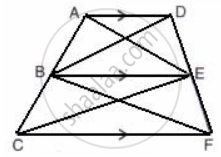
In the given figure, diagonals PR and QS of the parallelogram PQRS intersect at point O and LM is parallel to PS. Show that: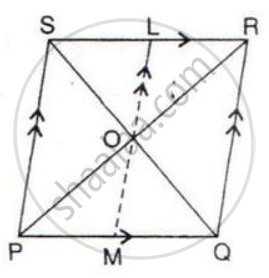
(i) 2 Area (POS) = Area (// gm PMLS)
(ii) Area (POS) + Area (QOR) = Area (// gm PQRS)
(iii) Area (POS) + Area (QOR) = Area (POQ) + Area (SOR).
In parallelogram ABCD, P is a point on side AB and Q is a point on side BC.
Prove that:
(i) ΔCPD and ΔAQD are equal in the area.
(ii) Area (ΔAQD) = Area (ΔAPD) + Area (ΔCPB)
In the following figure, DE is parallel to BC.
Show that:
(i) Area ( ΔADC ) = Area( ΔAEB ).
(ii) Area ( ΔBOD ) = Area( ΔCOE ).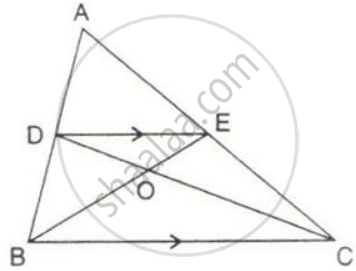
In the following figure, CE is drawn parallel to diagonals DB of the quadrilateral ABCD which meets AB produced at point E.
Prove that ΔADE and quadrilateral ABCD are equal in area.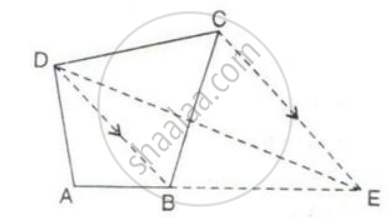
E, F, G, and H are the midpoints of the sides of a parallelogram ABCD.
Show that the area of quadrilateral EFGH is half of the area of parallelogram ABCD.
In parallelogram ABCD, P is the mid-point of AB. CP and BD intersect each other at point O. If the area of ΔPOB = 40 cm2, and OP: OC = 1:2, find:
(i) Areas of ΔBOC and ΔPBC
(ii) Areas of ΔABC and parallelogram ABCD.
Show that:
The ratio of the areas of two triangles on the same base is equal to the ratio of their heights.
