Advertisements
Advertisements
प्रश्न
In parallelogram ABCD, E is a point in AB and DE meets diagonal AC at point F. If DF: FE = 5:3 and area of ΔADF is 60 cm2; find
(i) area of ΔADE.
(ii) if AE: EB = 4:5, find the area of ΔADB.
(iii) also, find the area of parallelogram ABCD.
उत्तर
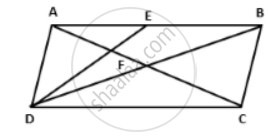
ΔADF and ΔAFE have the same vertex A and their bases are on the same straight line DE.
∴ `"A(ΔADF)"/"A(ΔAFE)" = "DF"/"FE"`
⇒ `60/"A(ΔAFE)" = 5/3 `
⇒ A(ΔAFE) = `( 60 xx 3 )/5` = 36cm2.
Now, A(ΔADE) = A(ΔADF) + A(ΔAFE) = 60 + 36 = 96 cm2.
ΔADE and ΔEDB have the same vertex D and their bases are on the same straight line AB.\
∴ `"A( ΔADE )"/"A( ΔEDB )" = "AE"/"EB"`
⇒ `96/"A( ΔEDB )" = 4/5`
⇒ A( ΔEDB ) = `( 96 xx 5 )/4` = 120 cm2 .
Now, A( ΔADB ) and ||m ABCD are on the same base AB and between the same parallels AB and DC.
∴ A( ΔADB ) = `1/2` A( ||m ABCD )
⇒ 216 = `1/2` A( ||m ABCD )
⇒ A( ||m ABCD ) = 2 x 216 = 432 cm2 .
APPEARS IN
संबंधित प्रश्न
In the given figure, ABCD is a parallelogram; BC is produced to point X.
Prove that: area ( Δ ABX ) = area (`square`ACXD )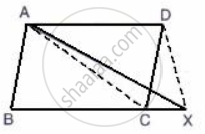
In the given figure, diagonals PR and QS of the parallelogram PQRS intersect at point O and LM is parallel to PS. Show that: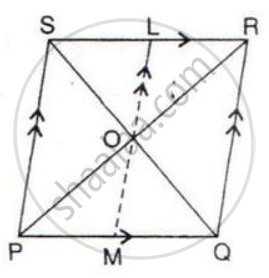
(i) 2 Area (POS) = Area (// gm PMLS)
(ii) Area (POS) + Area (QOR) = Area (// gm PQRS)
(iii) Area (POS) + Area (QOR) = Area (POQ) + Area (SOR).
In the following figure, DE is parallel to BC.
Show that:
(i) Area ( ΔADC ) = Area( ΔAEB ).
(ii) Area ( ΔBOD ) = Area( ΔCOE ).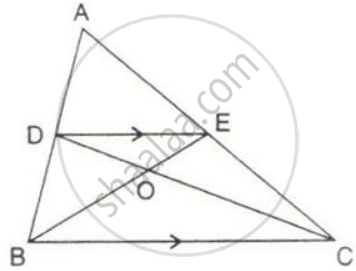
ABCD is a parallelogram a line through A cuts DC at point P and BC produced at Q. Prove that triangle BCP is equal in area to triangle DPQ.
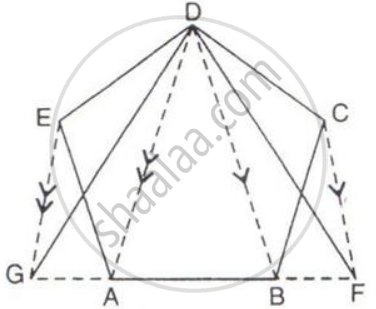
The given figure shows a pentagon ABCDE. EG drawn parallel to DA meets BA produced at G and CF draw parallel to DB meets AB produced at F.
Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.
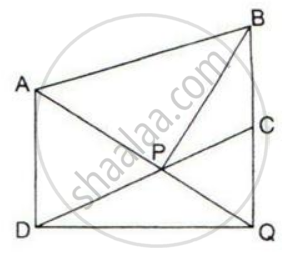
In a parallelogram ABCD, point P lies in DC such that DP: PC = 3:2. If the area of ΔDPB = 30 sq. cm.
find the area of the parallelogram ABCD.
ABCD is a parallelogram. P and Q are the mid-points of sides AB and AD respectively.
Prove that area of triangle APQ = `1/8` of the area of parallelogram ABCD.
E, F, G, and H are the midpoints of the sides of a parallelogram ABCD.
Show that the area of quadrilateral EFGH is half of the area of parallelogram ABCD.
Show that:
The ratio of the areas of two triangles of the same height is equal to the ratio of their bases.
Show that:
The ratio of the areas of two triangles on the same base is equal to the ratio of their heights.
