Advertisements
Advertisements
प्रश्न
In a parallelogram ABCD, point P lies in DC such that DP: PC = 3:2. If the area of ΔDPB = 30 sq. cm.
find the area of the parallelogram ABCD.
उत्तर
The ratio of the area of triangles with the same vertex and bases along the same line is equal to the ratio of their respective bases. So, we have
`"Area of DPB"/"Area of PCB" = "DP"/"PC" = 3/2`
Given: Area of ΔDPB = 30 sq. cm
Let 'x' be the area of the triangle PCB
Therefore, We have,
⇒ `30/x = 3/2`
⇒ x = `30/3 xx 2` = 20 sq.cm.
So area of ΔPCB = 20 sq. cm
Consider the following figure.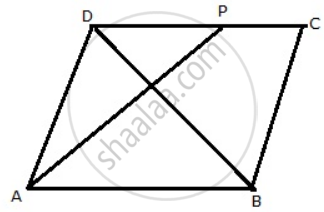
From the diagram, it is clear that,
Area( ΔCDB ) = Area( ΔDPB ) + Area( ΔCDB )
= 30 + 20 = 50 sq.cm.
The diagonal of the parallelogram divides it into two triangles ΔADB and ΔCDB of equal area.
Therefore,
Area( parallelogram ABCD ) = 2 x ΔCDB = 2 x 50 = 100 sq.cm.
APPEARS IN
संबंधित प्रश्न
In the given figure, AD // BE // CF.
Prove that area (ΔAEC) = area (ΔDBF)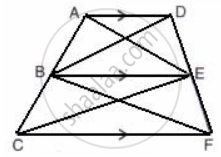
In the following, AC // PS // QR and PQ // DB // SR.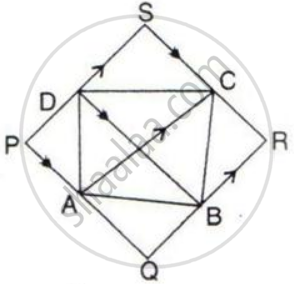
Prove that: Area of quadrilateral PQRS = 2 x Area of the quad. ABCD.
In the given figure, diagonals PR and QS of the parallelogram PQRS intersect at point O and LM is parallel to PS. Show that: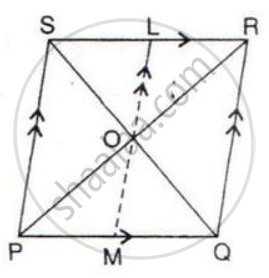
(i) 2 Area (POS) = Area (// gm PMLS)
(ii) Area (POS) + Area (QOR) = Area (// gm PQRS)
(iii) Area (POS) + Area (QOR) = Area (POQ) + Area (SOR).
In the following figure, DE is parallel to BC.
Show that:
(i) Area ( ΔADC ) = Area( ΔAEB ).
(ii) Area ( ΔBOD ) = Area( ΔCOE ).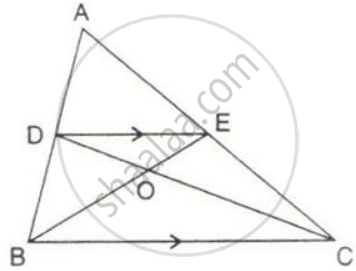
In the following figure, CE is drawn parallel to diagonals DB of the quadrilateral ABCD which meets AB produced at point E.
Prove that ΔADE and quadrilateral ABCD are equal in area.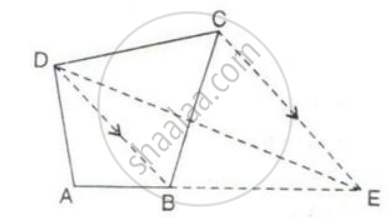
ABCD is a parallelogram a line through A cuts DC at point P and BC produced at Q. Prove that triangle BCP is equal in area to triangle DPQ.
E, F, G, and H are the midpoints of the sides of a parallelogram ABCD.
Show that the area of quadrilateral EFGH is half of the area of parallelogram ABCD.
In the following figure, BD is parallel to CA, E is mid-point of CA and BD = `1/2`CA
Prove that: ar. ( ΔABC ) = 2 x ar.( ΔDBC )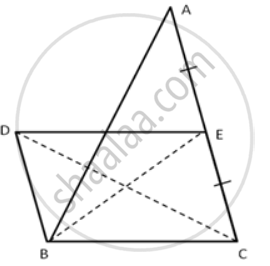
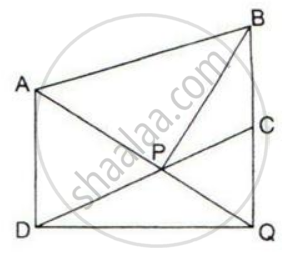
In parallelogram ABCD, P is the mid-point of AB. CP and BD intersect each other at point O. If the area of ΔPOB = 40 cm2, and OP: OC = 1:2, find:
(i) Areas of ΔBOC and ΔPBC
(ii) Areas of ΔABC and parallelogram ABCD.
Show that:
The ratio of the areas of two triangles on the same base is equal to the ratio of their heights.
