Advertisements
Advertisements
प्रश्न
In the following figure, BD is parallel to CA, E is mid-point of CA and BD = `1/2`CA
Prove that: ar. ( ΔABC ) = 2 x ar.( ΔDBC )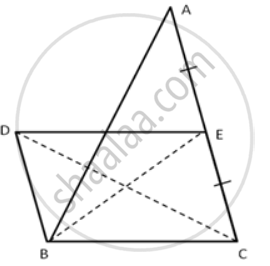
उत्तर
Here BCED is a parallelogram, Since BD = CE and BD || CE.
ar. ( ΔDBC ) = ar. ( ΔEBC ) ......( Since they have the same base and are between the same parallels )
In ΔABC,
BE is the median,
So, ar. ( ΔEBC ) = `1/2` ar. ( ΔABC )
Now, ar. ( ΔABC ) = ar. ( ΔEBC ) + ar. ( ΔABE)
Also, ar. ( ΔABC ) = 2ar. ( ΔEBC )
⇒ ar. ( ΔABC ) = 2ar. ( ΔDBC )
APPEARS IN
संबंधित प्रश्न
The given figure shows the parallelograms ABCD and APQR.
Show that these parallelograms are equal in the area.
[ Join B and R ]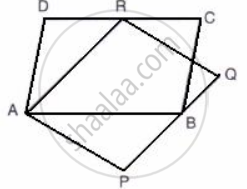
The given figure shows a rectangle ABDC and a parallelogram ABEF; drawn on opposite sides of AB.
Prove that:
(i) Quadrilateral CDEF is a parallelogram;
(ii) Area of the quad. CDEF
= Area of rect. ABDC + Area of // gm. ABEF.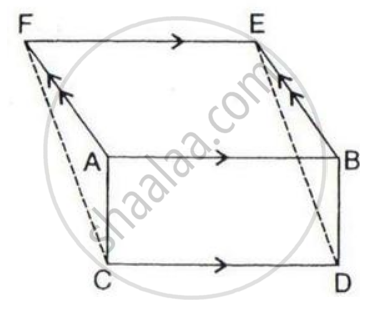
In the following, AC // PS // QR and PQ // DB // SR.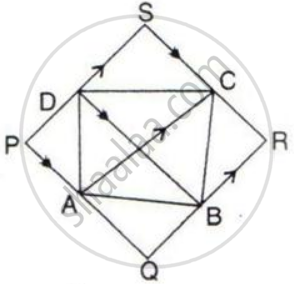
Prove that: Area of quadrilateral PQRS = 2 x Area of the quad. ABCD.
In the given figure, D is mid-point of side AB of ΔABC and BDEC is a parallelogram.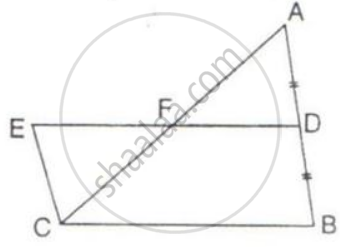
Prove that: Area of ABC = Area of // gm BDEC.
In the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD.
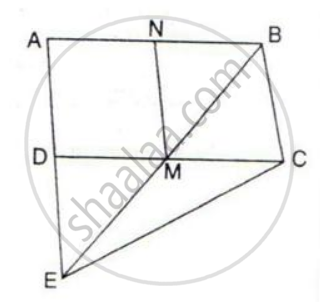
If the area of parallelogram ABCD is 48 cm2;
(i) State the area of the triangle BEC.
(ii) Name the parallelogram which is equal in area to the triangle BEC.
ABCD is a parallelogram a line through A cuts DC at point P and BC produced at Q. Prove that triangle BCP is equal in area to triangle DPQ.
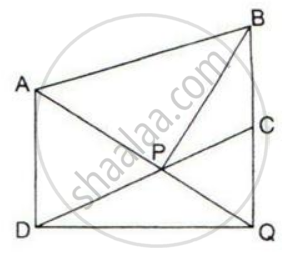
In a parallelogram ABCD, point P lies in DC such that DP: PC = 3:2. If the area of ΔDPB = 30 sq. cm.
find the area of the parallelogram ABCD.
ABCD is a parallelogram. P and Q are the mid-points of sides AB and AD respectively.
Prove that area of triangle APQ = `1/8` of the area of parallelogram ABCD.
E, F, G, and H are the midpoints of the sides of a parallelogram ABCD.
Show that the area of quadrilateral EFGH is half of the area of parallelogram ABCD.
Show that:
The ratio of the areas of two triangles on the same base is equal to the ratio of their heights.
