Advertisements
Advertisements
प्रश्न
In the given figure, D is mid-point of side AB of ΔABC and BDEC is a parallelogram.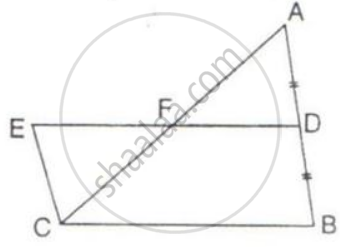
Prove that: Area of ABC = Area of // gm BDEC.
उत्तर
Here AD = DB and EC = DB, therefore EC = AD
Again,
∠EFC = ∠AFD .....( Opposite angles )
Since ED and CB are parallel lines and AC cut this line, therefore
∠ECF = ∠FAD
From the above conditions, we have
ΔEFC = ΔAFD
Adding quadrilateral CBDF in both sides, we have
Area of // gm BDEC = Area of ΔABC.
APPEARS IN
संबंधित प्रश्न
In the following, AC // PS // QR and PQ // DB // SR.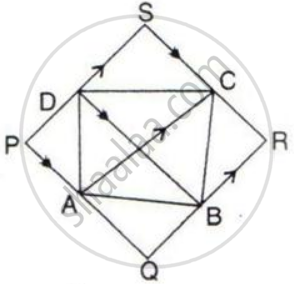
Prove that: Area of quadrilateral PQRS = 2 x Area of the quad. ABCD.
In the following figure, CE is drawn parallel to diagonals DB of the quadrilateral ABCD which meets AB produced at point E.
Prove that ΔADE and quadrilateral ABCD are equal in area.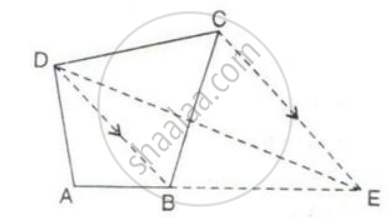
In the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC.
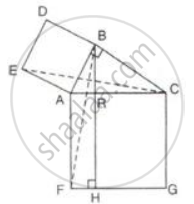
If BH is perpendicular to FG
prove that:
- ΔEAC ≅ ΔBAF
- Area of the square ABDE
- Area of the rectangle ARHF.
In the given figure, AP is parallel to BC, BP is parallel to CQ.
Prove that the area of triangles ABC and BQP are equal.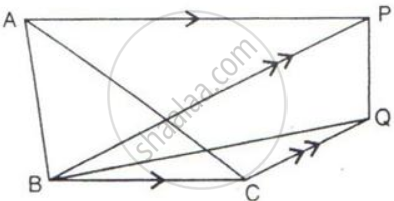
ABCD is a parallelogram a line through A cuts DC at point P and BC produced at Q. Prove that triangle BCP is equal in area to triangle DPQ.
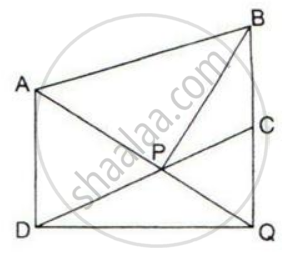
Show that:
A diagonal divides a parallelogram into two triangles of equal area.
In a parallelogram ABCD, point P lies in DC such that DP: PC = 3:2. If the area of ΔDPB = 30 sq. cm.
find the area of the parallelogram ABCD.
In parallelogram ABCD, E is a point in AB and DE meets diagonal AC at point F. If DF: FE = 5:3 and area of ΔADF is 60 cm2; find
(i) area of ΔADE.
(ii) if AE: EB = 4:5, find the area of ΔADB.
(iii) also, find the area of parallelogram ABCD.
In parallelogram ABCD, P is the mid-point of AB. CP and BD intersect each other at point O. If the area of ΔPOB = 40 cm2, and OP: OC = 1:2, find:
(i) Areas of ΔBOC and ΔPBC
(ii) Areas of ΔABC and parallelogram ABCD.
Show that:
The ratio of the areas of two triangles of the same height is equal to the ratio of their bases.
