Advertisements
Advertisements
प्रश्न
In the given figure, AD // BE // CF.
Prove that area (ΔAEC) = area (ΔDBF)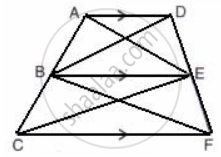
उत्तर
We know that the area of triangles on the same base and between the same parallel lines are equal.
Consider ABED quadrilateral; AD || BE.
With the common base, BE and between AD and BE parallel lines, we have
Area of ΔABE = Area of ΔBDE
Similarly, in BEFC quadrilateral, BE || CF
With common base BC and between BE and CF parallel lines, we have
Area of ΔBEC = Area of ΔBEF
Adding both equations, we have
Area of ΔABE + Area of ΔBEC = Area of ΔBEF + Area of ΔBDE
⇒ Area of AEC = Area of DBF
Hence Proved.
APPEARS IN
संबंधित प्रश्न
The given figure shows a rectangle ABDC and a parallelogram ABEF; drawn on opposite sides of AB.
Prove that:
(i) Quadrilateral CDEF is a parallelogram;
(ii) Area of the quad. CDEF
= Area of rect. ABDC + Area of // gm. ABEF.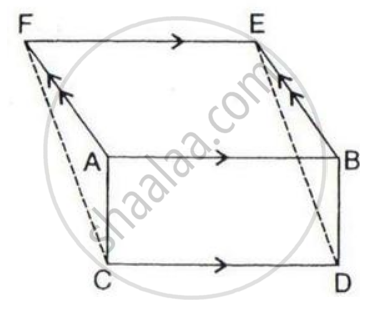
In the given figure, ABCD is a parallelogram; BC is produced to point X.
Prove that: area ( Δ ABX ) = area (`square`ACXD )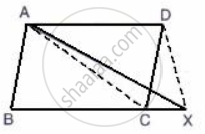
ABCD and BCFE are parallelograms. If area of triangle EBC = 480 cm2; AB = 30 cm and BC = 40 cm.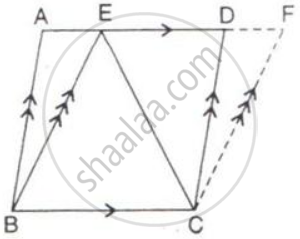
Calculate :
(i) Area of parallelogram ABCD;
(ii) Area of the parallelogram BCFE;
(iii) Length of altitude from A on CD;
(iv) Area of triangle ECF.
In the following figure, CE is drawn parallel to diagonals DB of the quadrilateral ABCD which meets AB produced at point E.
Prove that ΔADE and quadrilateral ABCD are equal in area.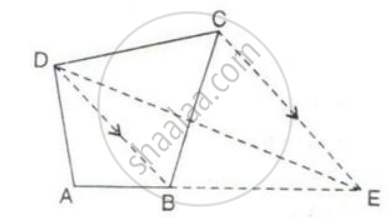
ABCD is a parallelogram a line through A cuts DC at point P and BC produced at Q. Prove that triangle BCP is equal in area to triangle DPQ.
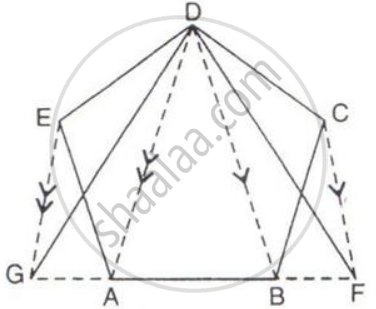
The given figure shows a pentagon ABCDE. EG drawn parallel to DA meets BA produced at G and CF draw parallel to DB meets AB produced at F.
Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.
In a parallelogram ABCD, point P lies in DC such that DP: PC = 3:2. If the area of ΔDPB = 30 sq. cm.
find the area of the parallelogram ABCD.
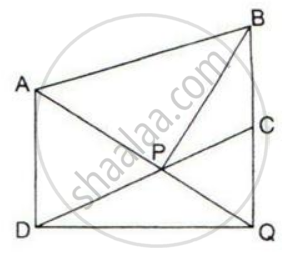
ABCD is a parallelogram. P and Q are the mid-points of sides AB and AD respectively.
Prove that area of triangle APQ = `1/8` of the area of parallelogram ABCD.
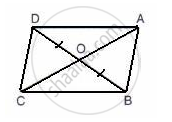
In the given figure, the diagonals AC and BD intersect at point O. If OB = OD and AB//DC,
show that:
(i) Area (Δ DOC) = Area (Δ AOB).
(ii) Area (Δ DCB) = Area (Δ ACB).
(iii) ABCD is a parallelogram.
In parallelogram ABCD, P is the mid-point of AB. CP and BD intersect each other at point O. If the area of ΔPOB = 40 cm2, and OP: OC = 1:2, find:
(i) Areas of ΔBOC and ΔPBC
(ii) Areas of ΔABC and parallelogram ABCD.
