Advertisements
Advertisements
प्रश्न
ABCD is a trapezium with AB // DC. A line parallel to AC intersects AB at point M and BC at point N.
Prove that: area of Δ ADM = area of Δ ACN.
उत्तर
Given: ABCD is a trapezium.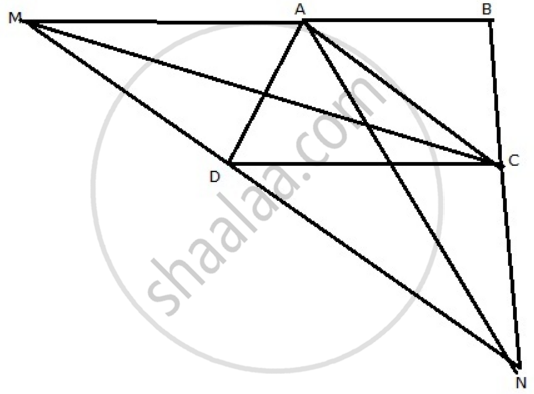
AB || CD, MN || AC
Join C and M
We know that the area of triangles on the same base and between the same parallel lines are equal.
So Area of ΔAMD = Area of ΔAMC
Similarly, consider the AMNC quadrilateral where MN || AC.
ΔACM and ΔACN are on the same base and between the same parallel lines. So areas are equal.
So, Area of ΔACM = Area of ΔCAN
From the above two equations, we can say
Area of ΔADM = Area of ΔCAN
Hence Proved.
APPEARS IN
संबंधित प्रश्न
The given figure shows the parallelograms ABCD and APQR.
Show that these parallelograms are equal in the area.
[ Join B and R ]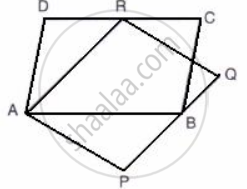
In the following, AC // PS // QR and PQ // DB // SR.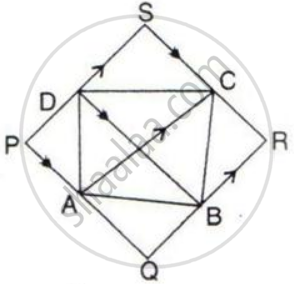
Prove that: Area of quadrilateral PQRS = 2 x Area of the quad. ABCD.
In the given figure, D is mid-point of side AB of ΔABC and BDEC is a parallelogram.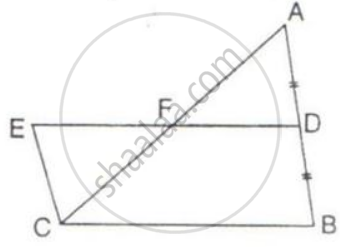
Prove that: Area of ABC = Area of // gm BDEC.
ABCD and BCFE are parallelograms. If area of triangle EBC = 480 cm2; AB = 30 cm and BC = 40 cm.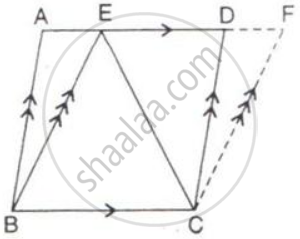
Calculate :
(i) Area of parallelogram ABCD;
(ii) Area of the parallelogram BCFE;
(iii) Length of altitude from A on CD;
(iv) Area of triangle ECF.
In parallelogram ABCD, P is a point on side AB and Q is a point on side BC.
Prove that:
(i) ΔCPD and ΔAQD are equal in the area.
(ii) Area (ΔAQD) = Area (ΔAPD) + Area (ΔCPB)
In the following figure, DE is parallel to BC.
Show that:
(i) Area ( ΔADC ) = Area( ΔAEB ).
(ii) Area ( ΔBOD ) = Area( ΔCOE ).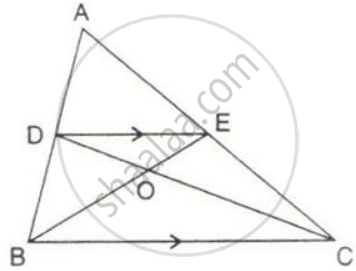
In the following figure, CE is drawn parallel to diagonals DB of the quadrilateral ABCD which meets AB produced at point E.
Prove that ΔADE and quadrilateral ABCD are equal in area.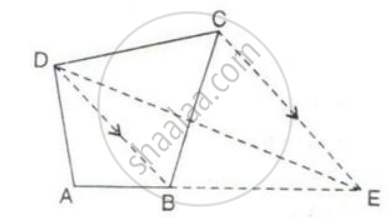
In the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC.
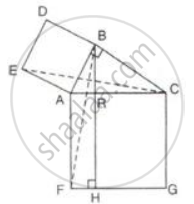
If BH is perpendicular to FG
prove that:
- ΔEAC ≅ ΔBAF
- Area of the square ABDE
- Area of the rectangle ARHF.
The given figure shows a pentagon ABCDE. EG drawn parallel to DA meets BA produced at G and CF draw parallel to DB meets AB produced at F.
Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.
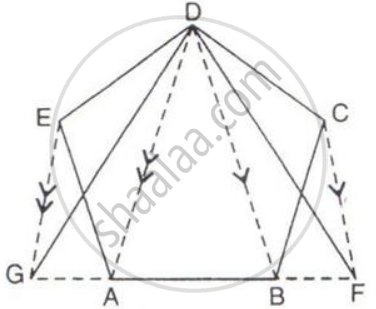
Show that:
The ratio of the areas of two triangles on the same base is equal to the ratio of their heights.
