Advertisements
Advertisements
प्रश्न
ABCD is a parallelogram in which BC is produced to E such that CE = BC and AE intersects CD at F.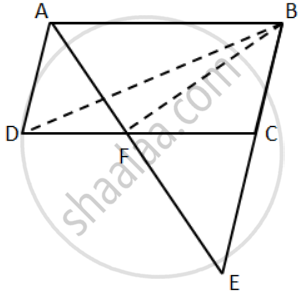
If ar.(∆DFB) = 30 cm2; find the area of parallelogram.
उत्तर
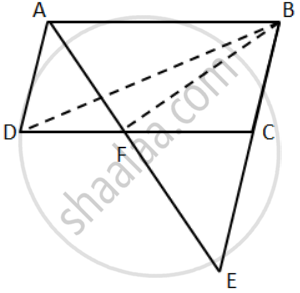
BC = CE .....( given )
Also, in parallelogram ABCD, BC = AD
⇒ AD = CE
Now, in ΔADF and ΔECF, We have
AD = CE
∠ADF = ∠ECF .....( Alternate angles )
∠DAF = ∠CEF ......( Alternate angles )
∴ ΔADF ≅ ΔECF ......( ASA Criterion )
⇒ Area( ΔADF ) = Area( ΔECF ) ....(1)
Also, in ΔFBE, FC is the median ....( Since BC = CE )
⇒ Area( ΔBCF ) = Area( ΔECF ) .....(2)
From (1) and (2)
Area( ΔADF ) = Area( ΔBCF ) ......(3)
Again, ΔADF and ΔBDF are on the base DF and between parallels DF and AB.
⇒ Area( ΔBDF ) = Area( ΔADF ) ........(4)
From (3) and (4),
Area( ΔBDF ) = Area( ΔBCF ) = 30 cm2
Area( ΔBCD ) = Area( ΔBDF ) + Area( ΔBCF ) = 30 + 30 = 60 cm2
Hence, Area of parallelogram ABCD = 2 x Area( ΔBCD ) = 2 x 60 = 120cm2.
APPEARS IN
संबंधित प्रश्न
The given figure shows the parallelograms ABCD and APQR.
Show that these parallelograms are equal in the area.
[ Join B and R ]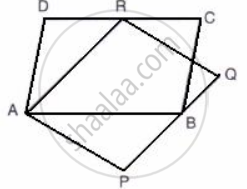
ABCD is a trapezium with AB // DC. A line parallel to AC intersects AB at point M and BC at point N.
Prove that: area of Δ ADM = area of Δ ACN.
ABCD and BCFE are parallelograms. If area of triangle EBC = 480 cm2; AB = 30 cm and BC = 40 cm.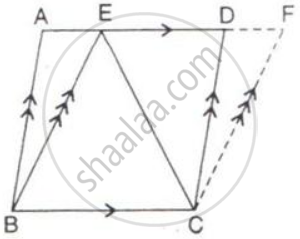
Calculate :
(i) Area of parallelogram ABCD;
(ii) Area of the parallelogram BCFE;
(iii) Length of altitude from A on CD;
(iv) Area of triangle ECF.
In parallelogram ABCD, P is a point on side AB and Q is a point on side BC.
Prove that:
(i) ΔCPD and ΔAQD are equal in the area.
(ii) Area (ΔAQD) = Area (ΔAPD) + Area (ΔCPB)
ABCD is a parallelogram a line through A cuts DC at point P and BC produced at Q. Prove that triangle BCP is equal in area to triangle DPQ.
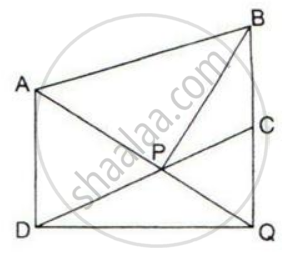
ABCD is a trapezium with AB parallel to DC. A line parallel to AC intersects AB at X and BC at Y.
Prove that the area of ∆ADX = area of ∆ACY.
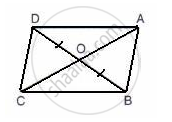
In the given figure, the diagonals AC and BD intersect at point O. If OB = OD and AB//DC,
show that:
(i) Area (Δ DOC) = Area (Δ AOB).
(ii) Area (Δ DCB) = Area (Δ ACB).
(iii) ABCD is a parallelogram.
E, F, G, and H are the midpoints of the sides of a parallelogram ABCD.
Show that the area of quadrilateral EFGH is half of the area of parallelogram ABCD.
The given figure shows a parallelogram ABCD with area 324 sq. cm. P is a point in AB such that AP: PB = 1:2
Find The area of Δ APD.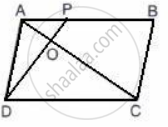
In parallelogram ABCD, P is the mid-point of AB. CP and BD intersect each other at point O. If the area of ΔPOB = 40 cm2, and OP: OC = 1:2, find:
(i) Areas of ΔBOC and ΔPBC
(ii) Areas of ΔABC and parallelogram ABCD.
