Advertisements
Advertisements
प्रश्न
The following figure shows a triangle ABC in which P, Q, and R are mid-points of sides AB, BC and CA respectively. S is mid-point of PQ:
Prove that: ar. ( ∆ ABC ) = 8 × ar. ( ∆ QSB )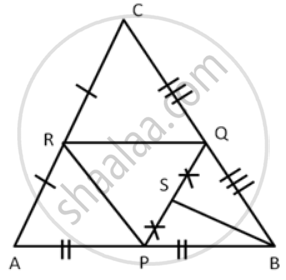
उत्तर
In ΔABC,
R and Q are the mid-points of AC and BC respectively.
⇒ RQ || AB
that is RQ || PB
So, area ( ΔPBQ ) = area( ΔAPR ) ....(i)( Since AP = PB and triangles on the same base and between the same parallels are equal in area. )
Since P and R are the mid-points of AB and AC respectively.
⇒ PR || BC
that is PR || BQ
So, quadrilateral PMQR is a parallelogram.
Also, area( ΔPBQ ) = area( ΔPQR ) ....(ii)( diagonal of a parallelogram divide the parallelogram into two triangles with the equal area )
From (i) and (ii)
area( ΔPQR ) = area ( ΔPBQ ) = area( ΔAPR ) ....(iii)
Similarly, P and Q are the mid-points of AB and BC respectively.
⇒ PQ || AC
that is PQ || RC
So, quadrilateral PQRC is a parallelogram.
Also, area( ΔRQC ) = area( ΔPQR ) .....(iv)( diagonal of a parallelogram divide the parallelogram into two triangles with the equal area )
From (iii) and (iv),
area( ΔPQR ) = area( ΔPBQ ) = area( ΔRQC ) = area( ΔAPR )
So, area( ΔPBQ ) = `1/4` area( ΔABC ) ....(v)
Also, since S is the mid-point of PQ,
BS is the median of ΔPBQ
SO, area( ΔQSB ) = `1/2`area( ΔPBQ )
From (v),
area( ΔQSB ) = `1/2 xx 1/4` area( ΔABC )
⇒ area( ΔABC ) = 8 area( ΔQSB ).
APPEARS IN
संबंधित प्रश्न
In the given figure; AD is median of ΔABC and E is any point on median AD.
Prove that Area (ΔABE) = Area (ΔACE).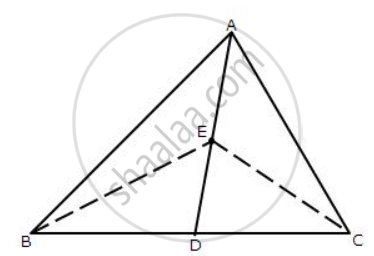
In the figure of question 2, if E is the mid-point of median AD, then
prove that:
Area (ΔABE) = `1/4` Area (ΔABC).
The base BC of triangle ABC is divided at D so that BD = `1/2`DC.
Prove that area of ΔABD = `1/3` of the area of ΔABC.
In the following figure, OAB is a triangle and AB || DC.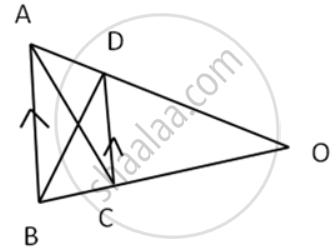
If the area of ∆ CAD = 140 cm2 and the area of ∆ ODC = 172 cm2,
find : (i) the area of ∆ DBC
(ii) the area of ∆ OAC
(iii) the area of ∆ ODB.
