Advertisements
Advertisements
Question
In the given figure, if the area of triangle ADE is 60 cm2, state, given reason, the area of :
(i) Parallelogram ABED;
(ii) Rectangle ABCF;
(iii) Triangle ABE.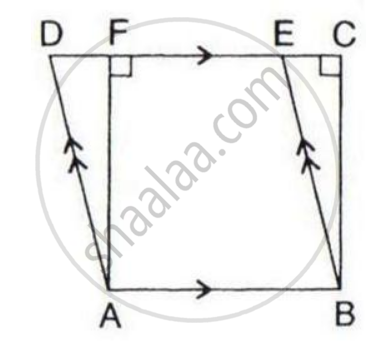
Solution
(i) ΔADE and parallelogram ABED are on the same base AB and between the same parallels DE//AB, so an area of the triangle ΔADE is half the area of parallelogram ABED.
Area of ABED = 2 (Area of ADE) = 120 cm2
(ii)Area of the parallelogram is equal to the area of a rectangle on the same base and of the same altitude i.e, between the same parallels
Area of ABCF = Area of ABED = 120 cm2
(iii)We know that area of triangles on the same base and between same parallel lines are equal
Area of ABE = Area of ADE = 60 cm2
APPEARS IN
RELATED QUESTIONS
In the given figure, AD // BE // CF.
Prove that area (ΔAEC) = area (ΔDBF)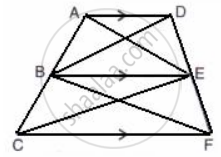
In the following, AC // PS // QR and PQ // DB // SR.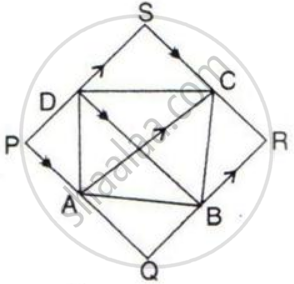
Prove that: Area of quadrilateral PQRS = 2 x Area of the quad. ABCD.
In the given figure, D is mid-point of side AB of ΔABC and BDEC is a parallelogram.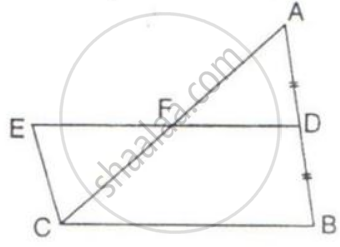
Prove that: Area of ABC = Area of // gm BDEC.
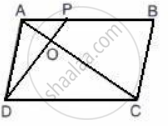
In the given figure, diagonals PR and QS of the parallelogram PQRS intersect at point O and LM is parallel to PS. Show that: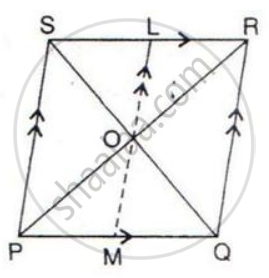
(i) 2 Area (POS) = Area (// gm PMLS)
(ii) Area (POS) + Area (QOR) = Area (// gm PQRS)
(iii) Area (POS) + Area (QOR) = Area (POQ) + Area (SOR).
In the following figure, DE is parallel to BC.
Show that:
(i) Area ( ΔADC ) = Area( ΔAEB ).
(ii) Area ( ΔBOD ) = Area( ΔCOE ).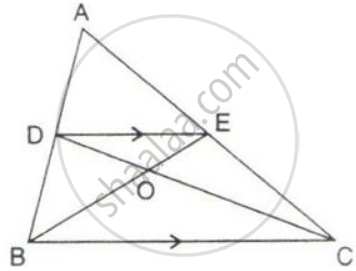
In the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD.
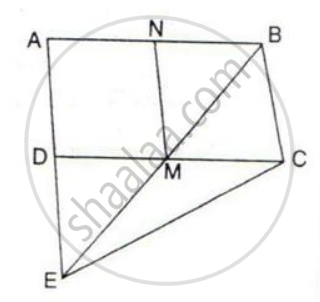
If the area of parallelogram ABCD is 48 cm2;
(i) State the area of the triangle BEC.
(ii) Name the parallelogram which is equal in area to the triangle BEC.
In the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC.
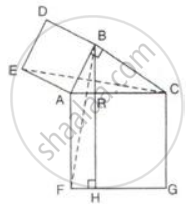
If BH is perpendicular to FG
prove that:
- ΔEAC ≅ ΔBAF
- Area of the square ABDE
- Area of the rectangle ARHF.
ABCD is a parallelogram. P and Q are the mid-points of sides AB and AD respectively.
Prove that area of triangle APQ = `1/8` of the area of parallelogram ABCD.
E, F, G, and H are the midpoints of the sides of a parallelogram ABCD.
Show that the area of quadrilateral EFGH is half of the area of parallelogram ABCD.
The given figure shows a parallelogram ABCD with area 324 sq. cm. P is a point in AB such that AP: PB = 1:2
Find The area of Δ APD.