Advertisements
Advertisements
प्रश्न
In the given figure, if the area of triangle ADE is 60 cm2, state, given reason, the area of :
(i) Parallelogram ABED;
(ii) Rectangle ABCF;
(iii) Triangle ABE.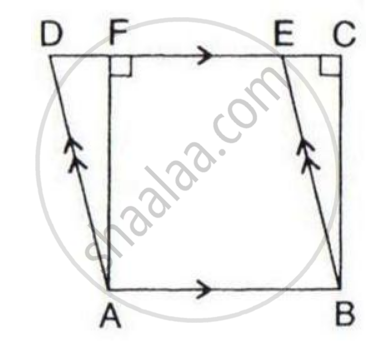
उत्तर
(i) ΔADE and parallelogram ABED are on the same base AB and between the same parallels DE//AB, so an area of the triangle ΔADE is half the area of parallelogram ABED.
Area of ABED = 2 (Area of ADE) = 120 cm2
(ii)Area of the parallelogram is equal to the area of a rectangle on the same base and of the same altitude i.e, between the same parallels
Area of ABCF = Area of ABED = 120 cm2
(iii)We know that area of triangles on the same base and between same parallel lines are equal
Area of ABE = Area of ADE = 60 cm2
APPEARS IN
संबंधित प्रश्न
The given figure shows the parallelograms ABCD and APQR.
Show that these parallelograms are equal in the area.
[ Join B and R ]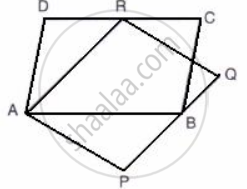
In the following, AC // PS // QR and PQ // DB // SR.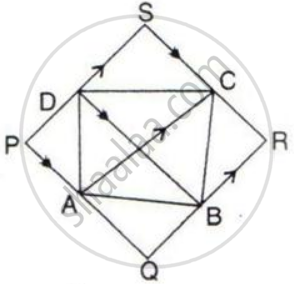
Prove that: Area of quadrilateral PQRS = 2 x Area of the quad. ABCD.
In parallelogram ABCD, P is a point on side AB and Q is a point on side BC.
Prove that:
(i) ΔCPD and ΔAQD are equal in the area.
(ii) Area (ΔAQD) = Area (ΔAPD) + Area (ΔCPB)
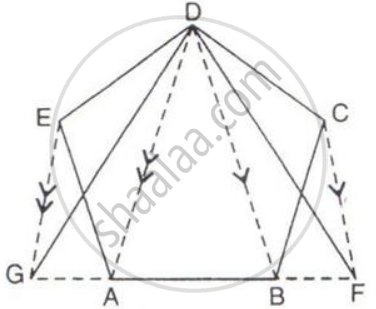
The given figure shows a pentagon ABCDE. EG drawn parallel to DA meets BA produced at G and CF draw parallel to DB meets AB produced at F.
Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.
E, F, G, and H are the midpoints of the sides of a parallelogram ABCD.
Show that the area of quadrilateral EFGH is half of the area of parallelogram ABCD.
In the following figure, BD is parallel to CA, E is mid-point of CA and BD = `1/2`CA
Prove that: ar. ( ΔABC ) = 2 x ar.( ΔDBC )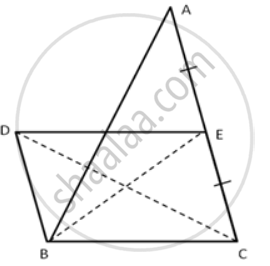
The given figure shows a parallelogram ABCD with area 324 sq. cm. P is a point in AB such that AP: PB = 1:2
Find The area of Δ APD.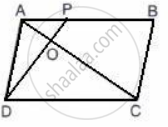
In parallelogram ABCD, E is a point in AB and DE meets diagonal AC at point F. If DF: FE = 5:3 and area of ΔADF is 60 cm2; find
(i) area of ΔADE.
(ii) if AE: EB = 4:5, find the area of ΔADB.
(iii) also, find the area of parallelogram ABCD.
Show that:
The ratio of the areas of two triangles of the same height is equal to the ratio of their bases.
Show that:
The ratio of the areas of two triangles on the same base is equal to the ratio of their heights.
