Advertisements
Advertisements
Question
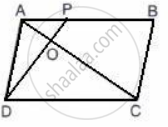
In the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC.
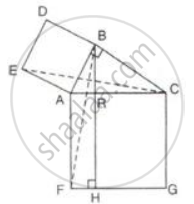
If BH is perpendicular to FG
prove that:
- ΔEAC ≅ ΔBAF
- Area of the square ABDE
- Area of the rectangle ARHF.
Solution
(i) ∠EAC = ∠EAB + ∠BAC
∠EAC = 90° + ∠BAC ...(i)
∠BAF = ∠FAC + ∠BAC
∠BAF = 90° + ∠BAC ...(ii)
From (i) and (ii), we get
∠EAC = ∠BAF
In ΔEAC and ΔBAF, we have, EA = AB
∠EAC = ∠BAF and AC = AF
∴ ΔEAC ≅ ΔBAF ...(SAS axiom of congruency)
(ii) Since ΔABC is a right triangle, We have,
AC2 = AB2 + BC2 ...(Using pythagoras theorm in ΔABC)
⇒ AB2 = AC2 - BC2
⇒ AB2 = (AR + RC)2 - (BR2 + RC2) ...(Since AC = AR + RC and Using Pythagoras Theorem in ΔBRC)
⇒ AB2 = AR2 + 2AR × RC + RC2 - (BR2 + RC2) ...(Using the identity)
⇒ AB2 = AR2 + 2AR × RC + RC2 - (AB2 - AR2 + RC2) ...(Using Pythagoras Theorem in ΔABR)
⇒ 2AB2 = 2AR2 + 2AR × RC
⇒ AB2 = AR(AR + RC)
⇒ AB2 = AR × AC
⇒ AB2 = AR × AF
⇒ Area (`square`ABDE) = Area(rectangle ARHF).
APPEARS IN
RELATED QUESTIONS
The given figure shows the parallelograms ABCD and APQR.
Show that these parallelograms are equal in the area.
[ Join B and R ]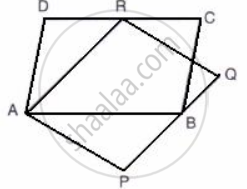
The given figure shows a rectangle ABDC and a parallelogram ABEF; drawn on opposite sides of AB.
Prove that:
(i) Quadrilateral CDEF is a parallelogram;
(ii) Area of the quad. CDEF
= Area of rect. ABDC + Area of // gm. ABEF.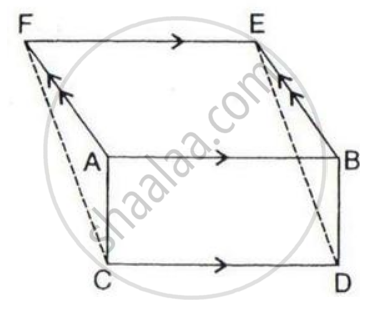
In the given figure, ABCD is a parallelogram; BC is produced to point X.
Prove that: area ( Δ ABX ) = area (`square`ACXD )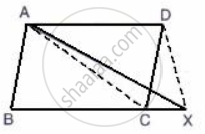
In the given figure, diagonals PR and QS of the parallelogram PQRS intersect at point O and LM is parallel to PS. Show that: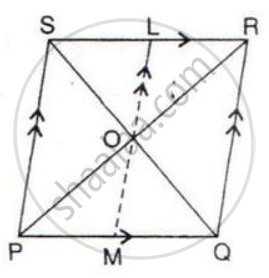
(i) 2 Area (POS) = Area (// gm PMLS)
(ii) Area (POS) + Area (QOR) = Area (// gm PQRS)
(iii) Area (POS) + Area (QOR) = Area (POQ) + Area (SOR).
In the following figure, DE is parallel to BC.
Show that:
(i) Area ( ΔADC ) = Area( ΔAEB ).
(ii) Area ( ΔBOD ) = Area( ΔCOE ).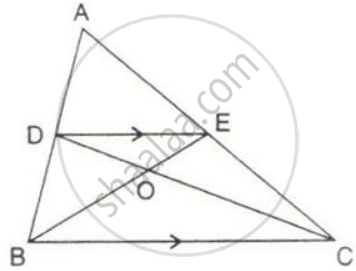
Show that:
A diagonal divides a parallelogram into two triangles of equal area.
ABCD is a parallelogram. P and Q are the mid-points of sides AB and AD respectively.
Prove that area of triangle APQ = `1/8` of the area of parallelogram ABCD.
E, F, G, and H are the midpoints of the sides of a parallelogram ABCD.
Show that the area of quadrilateral EFGH is half of the area of parallelogram ABCD.
In the following figure, BD is parallel to CA, E is mid-point of CA and BD = `1/2`CA
Prove that: ar. ( ΔABC ) = 2 x ar.( ΔDBC )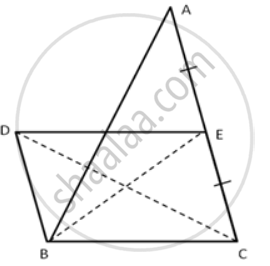
The given figure shows a parallelogram ABCD with area 324 sq. cm. P is a point in AB such that AP: PB = 1:2
Find The area of Δ APD.