Advertisements
Advertisements
प्रश्न
In the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC.
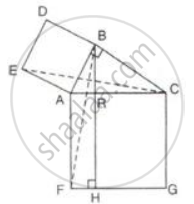
If BH is perpendicular to FG
prove that:
- ΔEAC ≅ ΔBAF
- Area of the square ABDE
- Area of the rectangle ARHF.
उत्तर
(i) ∠EAC = ∠EAB + ∠BAC
∠EAC = 90° + ∠BAC ...(i)
∠BAF = ∠FAC + ∠BAC
∠BAF = 90° + ∠BAC ...(ii)
From (i) and (ii), we get
∠EAC = ∠BAF
In ΔEAC and ΔBAF, we have, EA = AB
∠EAC = ∠BAF and AC = AF
∴ ΔEAC ≅ ΔBAF ...(SAS axiom of congruency)
(ii) Since ΔABC is a right triangle, We have,
AC2 = AB2 + BC2 ...(Using pythagoras theorm in ΔABC)
⇒ AB2 = AC2 - BC2
⇒ AB2 = (AR + RC)2 - (BR2 + RC2) ...(Since AC = AR + RC and Using Pythagoras Theorem in ΔBRC)
⇒ AB2 = AR2 + 2AR × RC + RC2 - (BR2 + RC2) ...(Using the identity)
⇒ AB2 = AR2 + 2AR × RC + RC2 - (AB2 - AR2 + RC2) ...(Using Pythagoras Theorem in ΔABR)
⇒ 2AB2 = 2AR2 + 2AR × RC
⇒ AB2 = AR(AR + RC)
⇒ AB2 = AR × AC
⇒ AB2 = AR × AF
⇒ Area (`square`ABDE) = Area(rectangle ARHF).
APPEARS IN
संबंधित प्रश्न
The given figure shows the parallelograms ABCD and APQR.
Show that these parallelograms are equal in the area.
[ Join B and R ]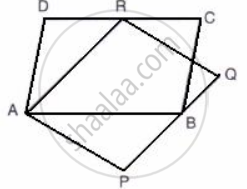
In the given figure, D is mid-point of side AB of ΔABC and BDEC is a parallelogram.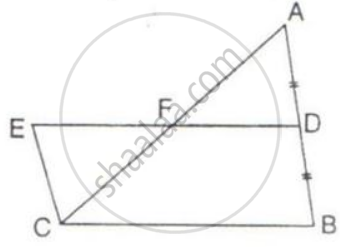
Prove that: Area of ABC = Area of // gm BDEC.
ABCD and BCFE are parallelograms. If area of triangle EBC = 480 cm2; AB = 30 cm and BC = 40 cm.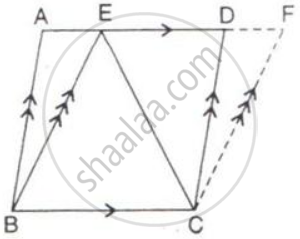
Calculate :
(i) Area of parallelogram ABCD;
(ii) Area of the parallelogram BCFE;
(iii) Length of altitude from A on CD;
(iv) Area of triangle ECF.
In parallelogram ABCD, P is a point on side AB and Q is a point on side BC.
Prove that:
(i) ΔCPD and ΔAQD are equal in the area.
(ii) Area (ΔAQD) = Area (ΔAPD) + Area (ΔCPB)
In the following figure, DE is parallel to BC.
Show that:
(i) Area ( ΔADC ) = Area( ΔAEB ).
(ii) Area ( ΔBOD ) = Area( ΔCOE ).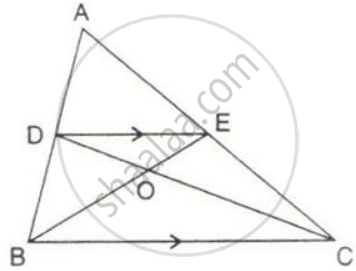
In the following figure, CE is drawn parallel to diagonals DB of the quadrilateral ABCD which meets AB produced at point E.
Prove that ΔADE and quadrilateral ABCD are equal in area.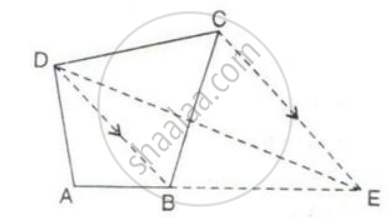
ABCD is a parallelogram a line through A cuts DC at point P and BC produced at Q. Prove that triangle BCP is equal in area to triangle DPQ.
E, F, G, and H are the midpoints of the sides of a parallelogram ABCD.
Show that the area of quadrilateral EFGH is half of the area of parallelogram ABCD.
In the following figure, BD is parallel to CA, E is mid-point of CA and BD = `1/2`CA
Prove that: ar. ( ΔABC ) = 2 x ar.( ΔDBC )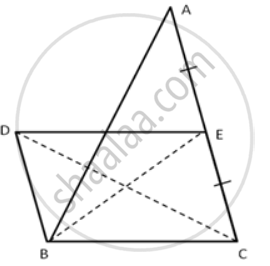
In ΔABC, E and F are mid-points of sides AB and AC respectively. If BF and CE intersect each other at point O,
prove that the ΔOBC and quadrilateral AEOF are equal in area.
