Advertisements
Advertisements
Question
The given figure shows a parallelogram ABCD with area 324 sq. cm. P is a point in AB such that AP: PB = 1:2
Find The area of Δ APD.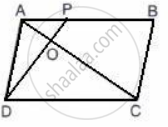
Solution
(i) The ratio of the area of triangles with the same vertex and bases along the same line is equal to the ratio of their respective bases.
So, we have
`["Area of "Δ"APD"]/["Area of" Δ"BPD" ] = "AP"/"BP"` = `1/2`
Area of parallelogram ABCD = 324 sq.cm
The area of the triangles with the same base and between the same parallels are equal.
We know that the area of the triangle is half the area of the parallelogram if they lie on the same base and between the parallels.
Therefore, we have,
Area ( ΔABD ) = `1/2` x Area [ || gm ABCD ]
=`324/2`
= 162 sq.cm
From the diagram it is clear that,
Area (Δ ABD ) = Area ( ΔAPD ) + Area ( ΔBPD )
⇒ 162 = Area ( ΔAPD ) + 2Area ( ΔAPD )
⇒ 162 = 3Area ( ΔAPD )
⇒ Area ( ΔAPD ) =`162/3`
⇒ Area ( ΔAPD ) = 54 sq.cm
(ii) Consider the triangle ΔAOP and ΔCOD
∠AOP = ∠COD ....[ vertically opposite angles ]
∠CDO = ∠APD .....[ AB and DC are parallel and DP is the transversal, alternate interior angles are equal ]
Thus, by Angle-Angle similarly,
ΔAOP ∼ ΔCOD.
Hence the corresponding sides are proportional.
`"AP"/"CD"= "OP"/"OD" = "AP"/"AB"`
= `"AP"/"AP + PB"`
= `"AP"/"3AP"`
=`1/3`
APPEARS IN
RELATED QUESTIONS
The given figure shows a rectangle ABDC and a parallelogram ABEF; drawn on opposite sides of AB.
Prove that:
(i) Quadrilateral CDEF is a parallelogram;
(ii) Area of the quad. CDEF
= Area of rect. ABDC + Area of // gm. ABEF.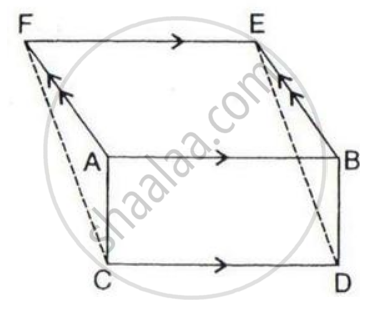
In the given figure, AD // BE // CF.
Prove that area (ΔAEC) = area (ΔDBF)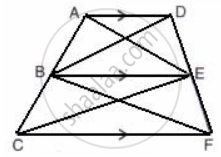
In parallelogram ABCD, P is a point on side AB and Q is a point on side BC.
Prove that:
(i) ΔCPD and ΔAQD are equal in the area.
(ii) Area (ΔAQD) = Area (ΔAPD) + Area (ΔCPB)
In the following figure, DE is parallel to BC.
Show that:
(i) Area ( ΔADC ) = Area( ΔAEB ).
(ii) Area ( ΔBOD ) = Area( ΔCOE ).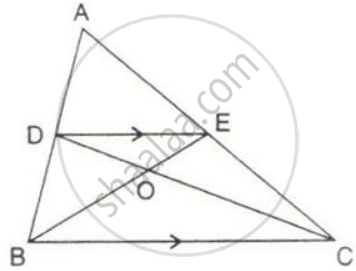
In the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC.
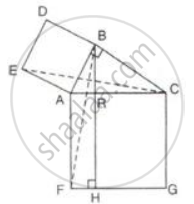
If BH is perpendicular to FG
prove that:
- ΔEAC ≅ ΔBAF
- Area of the square ABDE
- Area of the rectangle ARHF.
In the given figure, AP is parallel to BC, BP is parallel to CQ.
Prove that the area of triangles ABC and BQP are equal.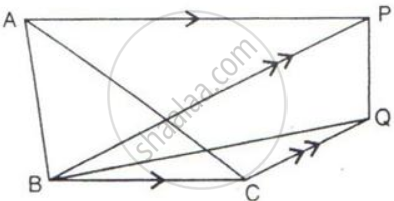
Show that:
A diagonal divides a parallelogram into two triangles of equal area.
E, F, G, and H are the midpoints of the sides of a parallelogram ABCD.
Show that the area of quadrilateral EFGH is half of the area of parallelogram ABCD.
In the following figure, BD is parallel to CA, E is mid-point of CA and BD = `1/2`CA
Prove that: ar. ( ΔABC ) = 2 x ar.( ΔDBC )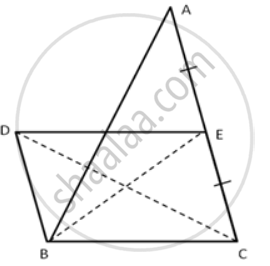
In parallelogram ABCD, P is the mid-point of AB. CP and BD intersect each other at point O. If the area of ΔPOB = 40 cm2, and OP: OC = 1:2, find:
(i) Areas of ΔBOC and ΔPBC
(ii) Areas of ΔABC and parallelogram ABCD.
