Advertisements
Advertisements
Question
In ΔABC, E and F are mid-points of sides AB and AC respectively. If BF and CE intersect each other at point O,
prove that the ΔOBC and quadrilateral AEOF are equal in area.
Solution
E and F are the midpoints of the sides AB and AC.
Consider the following figure.
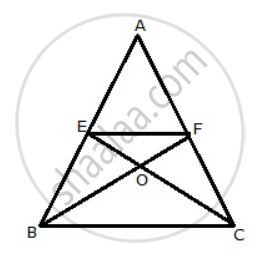
Therefore, by midpoint theorem, we have, EF || BC
Triangles BEF and CEF lie on the common base EF and between the parallels, EF and BC
Therefore, Ar.( ΔBEF ) = Ar.( ΔCOF )
⇒ Ar.( ΔBOE ) + Ar.( ΔEOF ) = Ar.( ΔEOF ) + Ar.( ΔCOF )
⇒ Ar.(ΔBOE ) = Ar.( ΔCOF )
Now BF and CE are the medians of the triangle ABC
Medians of the triangle divide it into two equal areas of triangles.
Thus, we have, Ar. (ΔABF) = Ar. (ΔCBF)
Subtracting Ar. ΔBOE on both the sides, we have
Ar. (ΔABF) - Ar. (ΔBOE) = Ar. (ΔCBF) - Ar. (ΔBOE)
Since, Ar. ( ΔBOE ) = Ar. ( ΔCOF ),
Ar. (ΔABF) - Ar. (ΔBOE) = Ar. (ΔCBF) - Ar. (ΔCOF)
Ar. ( quad. AEOF ) = Ar. ( ΔOBC ) , hence proved
APPEARS IN
RELATED QUESTIONS
The given figure shows the parallelograms ABCD and APQR.
Show that these parallelograms are equal in the area.
[ Join B and R ]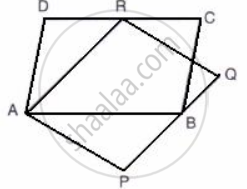
The given figure shows a rectangle ABDC and a parallelogram ABEF; drawn on opposite sides of AB.
Prove that:
(i) Quadrilateral CDEF is a parallelogram;
(ii) Area of the quad. CDEF
= Area of rect. ABDC + Area of // gm. ABEF.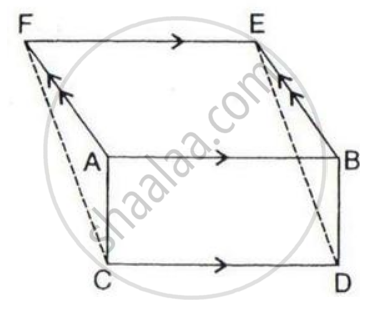
ABCD is a trapezium with AB // DC. A line parallel to AC intersects AB at point M and BC at point N.
Prove that: area of Δ ADM = area of Δ ACN.
In the following, AC // PS // QR and PQ // DB // SR.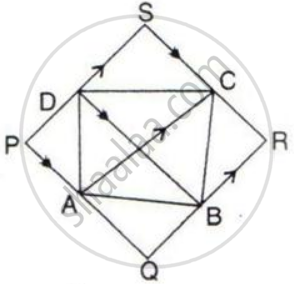
Prove that: Area of quadrilateral PQRS = 2 x Area of the quad. ABCD.
ABCD and BCFE are parallelograms. If area of triangle EBC = 480 cm2; AB = 30 cm and BC = 40 cm.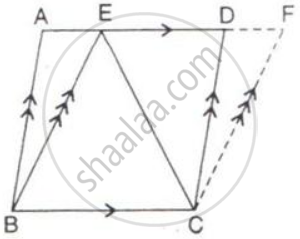
Calculate :
(i) Area of parallelogram ABCD;
(ii) Area of the parallelogram BCFE;
(iii) Length of altitude from A on CD;
(iv) Area of triangle ECF.
In the given figure, diagonals PR and QS of the parallelogram PQRS intersect at point O and LM is parallel to PS. Show that: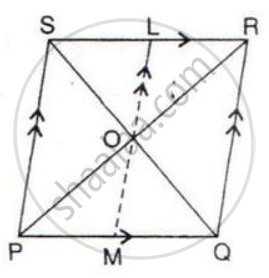
(i) 2 Area (POS) = Area (// gm PMLS)
(ii) Area (POS) + Area (QOR) = Area (// gm PQRS)
(iii) Area (POS) + Area (QOR) = Area (POQ) + Area (SOR).
In the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD.
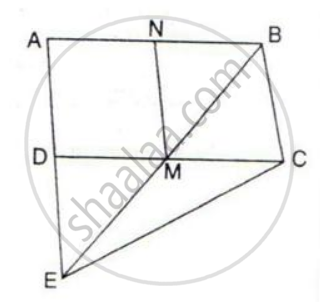
If the area of parallelogram ABCD is 48 cm2;
(i) State the area of the triangle BEC.
(ii) Name the parallelogram which is equal in area to the triangle BEC.
In the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC.
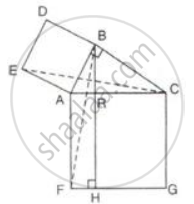
If BH is perpendicular to FG
prove that:
- ΔEAC ≅ ΔBAF
- Area of the square ABDE
- Area of the rectangle ARHF.
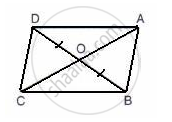
In the given figure, the diagonals AC and BD intersect at point O. If OB = OD and AB//DC,
show that:
(i) Area (Δ DOC) = Area (Δ AOB).
(ii) Area (Δ DCB) = Area (Δ ACB).
(iii) ABCD is a parallelogram.
Show that:
The ratio of the areas of two triangles on the same base is equal to the ratio of their heights.
