Advertisements
Advertisements
Question
ABCD is a trapezium with AB parallel to DC. A line parallel to AC intersects AB at X and BC at Y.
Prove that the area of ∆ADX = area of ∆ACY.
Solution
Join CX, DX and AY.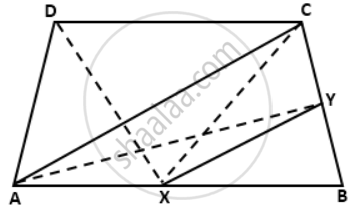
Now, triangles ADX and ACX are on the same base AX and between the parallels AB and DC.
∴ A( ΔADX ) = A( ΔACX ) ….(i)
Also, triangles ACX and ACY are on the same base AC and between the parallels AC and XY.
∴ A( ΔACX ) = A( ΔACY ) ….(ii)
From (i) and (ii), we get
A( ΔADX ) = A( ΔACY )
APPEARS IN
RELATED QUESTIONS
The given figure shows the parallelograms ABCD and APQR.
Show that these parallelograms are equal in the area.
[ Join B and R ]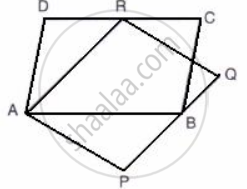
The given figure shows a rectangle ABDC and a parallelogram ABEF; drawn on opposite sides of AB.
Prove that:
(i) Quadrilateral CDEF is a parallelogram;
(ii) Area of the quad. CDEF
= Area of rect. ABDC + Area of // gm. ABEF.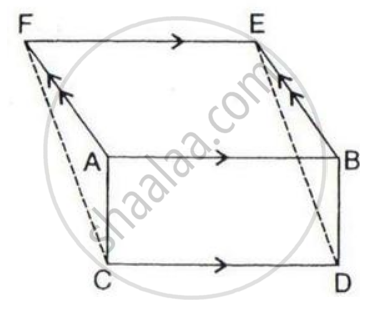
In the given figure, D is mid-point of side AB of ΔABC and BDEC is a parallelogram.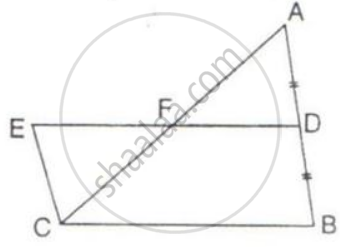
Prove that: Area of ABC = Area of // gm BDEC.
ABCD and BCFE are parallelograms. If area of triangle EBC = 480 cm2; AB = 30 cm and BC = 40 cm.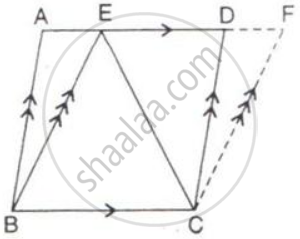
Calculate :
(i) Area of parallelogram ABCD;
(ii) Area of the parallelogram BCFE;
(iii) Length of altitude from A on CD;
(iv) Area of triangle ECF.
In parallelogram ABCD, P is a point on side AB and Q is a point on side BC.
Prove that:
(i) ΔCPD and ΔAQD are equal in the area.
(ii) Area (ΔAQD) = Area (ΔAPD) + Area (ΔCPB)
In the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD.
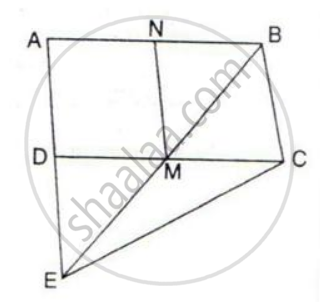
If the area of parallelogram ABCD is 48 cm2;
(i) State the area of the triangle BEC.
(ii) Name the parallelogram which is equal in area to the triangle BEC.
ABCD is a parallelogram a line through A cuts DC at point P and BC produced at Q. Prove that triangle BCP is equal in area to triangle DPQ.
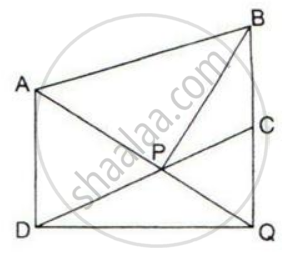
In a parallelogram ABCD, point P lies in DC such that DP: PC = 3:2. If the area of ΔDPB = 30 sq. cm.
find the area of the parallelogram ABCD.
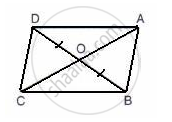
In the given figure, the diagonals AC and BD intersect at point O. If OB = OD and AB//DC,
show that:
(i) Area (Δ DOC) = Area (Δ AOB).
(ii) Area (Δ DCB) = Area (Δ ACB).
(iii) ABCD is a parallelogram.
In ΔABC, E and F are mid-points of sides AB and AC respectively. If BF and CE intersect each other at point O,
prove that the ΔOBC and quadrilateral AEOF are equal in area.
