Advertisements
Advertisements
Question
In the given figure; AD is median of ΔABC and E is any point on median AD.
Prove that Area (ΔABE) = Area (ΔACE).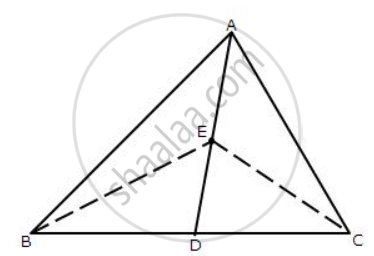
Solution
AD is the median of ΔABC. Therefore it will divide ΔABC into two triangles of equal areas.
∴ Area (ΔABD)= Area (ΔACD) ...(i)
ED is the median of ΔEBC
∴Area (ΔEBD)= Area (ΔECD) ...(ii)
Subtracting equation (ii) from (i), we obtain
Area (ΔABD)- Area (ΔEBD) = Area (ΔACD)- Area (ΔECD)
Area (ΔABE) = Area (ΔACE).
Hence proved
APPEARS IN
RELATED QUESTIONS
The following figure shows a triangle ABC in which P, Q, and R are mid-points of sides AB, BC and CA respectively. S is mid-point of PQ:
Prove that: ar. ( ∆ ABC ) = 8 × ar. ( ∆ QSB )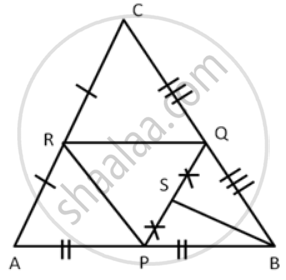
In the figure of question 2, if E is the mid-point of median AD, then
prove that:
Area (ΔABE) = `1/4` Area (ΔABC).
The base BC of triangle ABC is divided at D so that BD = `1/2`DC.
Prove that area of ΔABD = `1/3` of the area of ΔABC.
In the following figure, OAB is a triangle and AB || DC.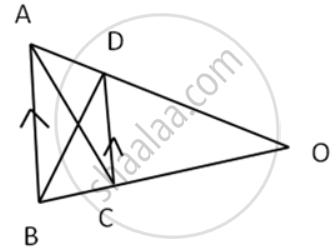
If the area of ∆ CAD = 140 cm2 and the area of ∆ ODC = 172 cm2,
find : (i) the area of ∆ DBC
(ii) the area of ∆ OAC
(iii) the area of ∆ ODB.
