Selina solutions for Concise Mathematics [English] Class 9 ICSE chapter 1 - Rational and Irrational Numbers [Latest edition]

Is zero a rational number ? Can it be written in the form `P/q`, where p and q are integers and q≠0 ?

Are the following statement true or false ? Give reason for your answer.

1. Every whole number is a natural number.
2. Every whole number is a rational number.
3. Every integer is a rational number.
4. Every rational number is a whole number.

Arrange `-5/9, 7/12, -2/3 and 11/18` in ascending order of their magnitudes.
Also, find the difference between the largest and smallest of these rational numbers. Express this difference as a decimal fraction correct to one decimal place.

Arrange `5/8, -3/16, -1/4 and 17/32` in descending order of their magnitudes.
Also, find the sum of the lowest and largest of these fractions. Express the result obtained as a decimal fraction correct to two decimal places.

Without doing any actual division, find which of the following rational numbers have terminating decimal representation:

`7/16`

Without doing any actual division, find which of the following rational numbers have terminating decimal representation : `23/125`

Without doing any actual division, find which of the following rational numbers have terminating decimal representation : `9/14`

Without doing any actual division, find which of the following rational numbers have terminating decimal representation : `32/45`

Without doing any actual division, find which of the following rational numbers have terminating decimal representation : `43/50`

Without doing any actual division, find which of the following rational numbers have terminating decimal representation : `17/40`

Without doing any actual division, find which of the following rational numbers have terminating decimal representation : `61/75`

Without doing any actual division, find which of the following rational numbers have terminating decimal representation : `123/250`

State, whether the following numbers is rational or not : ( 2 + √2 )²

State, whether the following numbers is rational or not : ( 3 - √3 )²

State, whether the following numbers is rational or not : ( 5 + √5 )( 5 - √5 )

State, whether the following numbers is rational or not:

(√3 - √2)²

State, whether the following numbers is rational or not : 
`( 3/[2sqrt2])^2`

State, whether the following number is rational or not :
`( [√7]/[6sqrt2])^2`

Find the square of : `[3sqrt5]/5`

Find the square of : √3 + √2

Find the square of : √5 - 2

Find the square of : 3 + 2√5

State, in each case, whether true or false : 
√2 + √3 = √5

State, in each case, whether true or false : 
2√4 + 2 = 6

State, in each case, whether true or false : 
3√7 - 2√7 = √7 

State, in each case, whether true or false : 
`2/7` ia an irrational number.

State, in each case, whether true or false :
`5/11` is a rational number.

State, in each case, whether true or false : 
All rational numbers are real numbers.

State, in each case, whether true or false : 
All real numbers are rational numbers.

State, in each case, whether true or false : 
Some real numbers are rational numbers.

Given universal set =
`{ -6, -5 3/4, -sqrt4, -3/5, -3/8, 0, 4/5, 1, 1 2/3, sqrt8, 3.01, π, 8.47 }`

From the given set, find: set of rational numbers

Given universal set =
`{ -6, -5 3/4, -sqrt4, -3/5, -3/8, 0, 4/5, 1, 1 2/3, sqrt8, 3.01, π, 8.47 }`

From the given set, find: set of irrational numbers

Given universal set =
`{ -6, -5 3/4, -sqrt4, -3/5, -3/8, 0, 4/5, 1, 1 2/3, sqrt8, 3.01, π, 8.47 }`

From the given set, find: set of integers

Given universal set =
`{ -6, -5 3/4, -sqrt4, -3/5, -3/8, 0, 4/5, 1, 1 2/3, sqrt8, 3.01, π, 8.47 }`
From the given set, find : set of non-negative integers

Prove that the following number is irrational: √3 + √2

Prove that the following number is irrational:  3 - √2

Prove that the following number is irrational: √5 - 2

Write a pair of irrational numbers whose sum is irrational.

Write a pair of irrational numbers whose sum is rational.

Write a pair of irrational numbers whose difference is irrational.

Write a pair of irrational numbers whose difference is rational.

Write a pair of irrational numbers whose product is irrational.

Write a pair of irrational numbers whose product is rational. 

Write in ascending order: 3√5 and 4√3

Write in ascending order :  `2 root(3)(5)  and 3 root(3)(2)`

Write in ascending order :  6√5, 7√3 and 8√2

Write in ascending order : 6√5, 7√3, and 8√2

Write in descending order:

`2 root(4)(6) and 3 root(4)(2)`

Write in descending order: 7√3 and 3√7

Compare: `root(6)(15) and root(4)(12)`

Compare : `sqrt24 and root(3)(35)`

Insert two irrational numbers between 5 and 6.

Insert five irrational numbers between `2sqrt5` and `3sqrt3`.

Write two rational numbers between √2 and √3.

Write three rational numbers between √3 and √5.

Simplify : `root(5)(16) xx root(5)(2)`

Simplify : `root(4)(243)/root(4)(3)`

Simplify : ( 3 + √2 )( 4 + √7 )

Simplify : (√3 - √2 )²

State, with reason, of the following is surd or not : √180

State, with reason, of the following is surd or not:

`root(4)(27)`

State, with reason, of the following is surd or not : 
`root(5)(128)`

State, with reason, of the following is surd or not : 
`root(3)(64)`

State, with reason, of the following is surd or not : 
`root(3)(25). root(3)(40)`

State, with reason, of the following is surd or not : 
`root(3)( -125 )`

State, with reason, of the following is surd or not: √π

State, with reason, of the following is surd or not : 
`sqrt( 3 + sqrt2 )`

Write the lowest rationalising factor of 5√2.

Write the lowest rationalising factor of : √24

Write the lowest rationalising factor of √5 - 3.

Write the lowest rationalising factor of : 7 - √7

Write the lowest rationalising factor of : √18 - √50

Write the lowest rationalising factor of : √5 - √2

Write the lowest rationalising factor of : √13 + 3

Write the lowest rationalising factor of : 15 - 3√2

Write the lowest rationalising factor of : 3√2 + 2√3

Rationalise the denominators of : `3/sqrt5`

Rationalise the denominators of : `(2sqrt3)/sqrt5`

Rationalise the denominators of : `1/(sqrt3 - sqrt2 )`

Rationalise the denominators of : `3/[ sqrt5 + sqrt2 ]`

Rationalise the denominators of : `[ 2 - √3 ]/[ 2 + √3 ]`

Rationalise the denominators of : `[ √3 + 1 ]/[ √3 - 1 ]`

Rationalise the denominators of : `[ sqrt3 - sqrt2 ]/[ sqrt3 + sqrt2 ]`

Rationalise the denominators of : `[sqrt6 - sqrt5]/[sqrt6 + sqrt5]`

Rationalise the denominators of : `[ 2√5 + 3√2 ]/[ 2√5 - 3√2 ]`

Find the values of 'a' and 'b' in each of the following : 
`[2 + sqrt3]/[ 2 - sqrt3 ] = a + bsqrt3`

Find the values of 'a' and 'b' in each of the following:
`( sqrt7 - 2 )/( sqrt7 + 2 ) = asqrt7 + b` 

Find the values of 'a' and 'b' in each of the following: 
`3/[ sqrt3 - sqrt2 ] = asqrt3 - bsqrt2`

Find the values of 'a' and 'b' in each of the following:
`[5 + 3sqrt2]/[ 5 - 3sqrt2] = a + bsqrt2`

Simplify :
` 22/[2sqrt3 + 1] + 17/[ 2sqrt3 - 1]`

Simplify:

`sqrt2/[sqrt6 - sqrt2] - sqrt3/[sqrt6 + sqrt2]`

If x =`[sqrt5 - 2 ]/[ sqrt5 + 2]` and y = `[ sqrt5 + 2]/[ sqrt5 - 2 ]`; find :
x²

If x =`[sqrt5 - 2 ]/[ sqrt5 + 2]` and y = `[ sqrt5 + 2]/[ sqrt5 - 2 ]`; find : y²

If x =`[sqrt5 - 2 ]/[ sqrt5 + 2]` and y = `[ sqrt5 + 2]/[ sqrt5 - 2 ]`; find :  xy

If x =`[sqrt5 - 2 ]/[ sqrt5 + 2]` and y = `[ sqrt5 + 2]/[ sqrt5 - 2]`; find:

x² + y² + xy.

If m = `1/[ 3 - 2sqrt2 ] and n = 1/[ 3 + 2sqrt2 ],` find m²

If m = `1/[ 3 - 2sqrt2 ] and n = 1/[ 3 + 2sqrt2 ],` find mn

If m = `1/[ 3 - 2sqrt2 ] and n = 1/[ 3 + 2sqrt2 ],` find n²

If x = `2sqrt3 + 2sqrt2`, find: `1/x`

If x = 2√3 + 2√2 , find : `(x + 1/x)`

If x = 2√3 + 2√2 , find : `( x + 1/x)^2`

If x = 1 - √2, find the value of `( x - 1/x )^3`

If x = 5 - 2√6, find `x^2 + 1/x^2`

Show that :
`1/[ 3 - 2√2] - 1/[ 2√2 - √7 ] + 1/[ √7 - √6 ] - 1/[ √6 - √5 ] + 1/[√5 - 2] = 5`

Rationalise the denominator of `1/[ √3 - √2 + 1]`

If √2 = 1.4 and √3 = 1.7, find the value of : `1/(√3 - √2)`

If √2 = 1.4 and √3 = 1.7, find the value of : `1/(3 + 2√2)`

If `sqrt2` = 1.4 and `sqrt3` = 1.7, find the value of `(2 - sqrt3)/(sqrt3).`

Evaluate : `( 4 - √5 )/( 4 + √5 ) + ( 4 + √5 )/( 4 - √5 )`

If `[ 2 + sqrt5 ]/[ 2 - sqrt5] = x and  [2 - sqrt5 ]/[ 2 + sqrt5] = y`; find the value of x² - y².

Simplify : `sqrt18/[ 5sqrt18 + 3sqrt72 - 2sqrt162]`

Simplify:

`(sqrt(x^2 + y^2) - y)/(x - sqrt(x^2 - y^2)) ÷ (sqrt(x^2 - y^2) + x)/(sqrt(x^2 + y^2) + y)`

Evaluate, correct to one place of decimal, the expression `5/(sqrt20 - sqrt10)`, if `sqrt5` = 2.2 and `sqrt10` = 3.2.

If x = `sqrt3 - sqrt2`, find the value of:

(i) `x + 1/x`

(ii) `x^2 + 1/x^2`

(iii) `x^3 + 1/x^3`

(iv) `x^3 + 1/x^3 - 3(x^2 + 1/x^2) + x + 1/x`

Show that Negative of an irrational number is irrational.

Show that the product of a non-zero rational number and an irrational number is an irrational number.

Draw a line segment of length `sqrt5` cm.

Draw a line segment of length `sqrt3` cm.

Draw a line segment of length `sqrt8` cm.

Show that: `(4 - sqrt5)/(4 + sqrt5) + 2/(5 + sqrt3) + (4 + sqrt5)/(4 - sqrt5) + 2/(5 - sqrt3) = 52/11`

Show that: `x^3 + 1/x^3 = 52`, if x = 2 + `sqrt3`

Show that: `x^2 + 1/x^2 = 34,` if x = 3 + `2sqrt2`

Show that: `(3sqrt2 - 2sqrt3)/(3sqrt2 + 2sqrt3) + (2 sqrt3)/(sqrt3 - sqrt2) = 11`

Show that x is irrational, if x² = 6.

Show that x is irrational, if x² = 0.009.

Show that x is irrational, if x² = 27.

Show that x is rational, if x² = 16.

Show that x is rational, if x² = 0.0004.

Show that x is rational, if x² = `1 7/9`

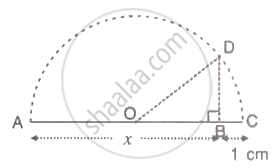
Using the following figure, show that BD = `sqrtx`.