Advertisements
Advertisements
Question
Draw a line segment of length `sqrt5` cm.
Solution
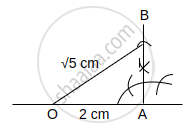
Construct a right-angled triangel OAB with
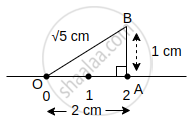
OA = 2 cm,
∠OAB = 90° and
AB = 1 cm
Using OB2 = OA2 + AB2
OB2 = 22 + 12
OB2 = 4 + 1
OB2 = 5
OB = `sqrt5`
APPEARS IN
RELATED QUESTIONS
Rationalize the denominator.
`2/(3 sqrt 7)`
Simplify the following
`(sqrt(5) - 2)/(sqrt(5) + 2) - (sqrt(5) + 2)/(sqrt(5) - 2)`
In the following, find the values of a and b:
`(1)/(sqrt(5) - sqrt(3)) = "a"sqrt(5) - "b"sqrt(3)`
In the following, find the value of a and b:
`(sqrt(3) - 1)/(sqrt(3) + 1) + (sqrt(3) + 1)/(sqrt(3) - 1) = "a" + "b"sqrt(3)`
If x = `(7 + 4sqrt(3))`, find the value of
`x^2 + (1)/x^2`
If x = `(4 - sqrt(15))`, find the values of
`(1)/x`
If x = `(4 - sqrt(15))`, find the values of
`x^2 + (1)/x^2`
If x = `sqrt3 - sqrt2`, find the value of:
(i) `x + 1/x`
(ii) `x^2 + 1/x^2`
(iii) `x^3 + 1/x^3`
(iv) `x^3 + 1/x^3 - 3(x^2 + 1/x^2) + x + 1/x`
Show that Negative of an irrational number is irrational.
Show that: `(3sqrt2 - 2sqrt3)/(3sqrt2 + 2sqrt3) + (2 sqrt3)/(sqrt3 - sqrt2) = 11`
