Advertisements
Advertisements
Question
In a ΔABC, D, E, F are the mid-points of sides BC, CA and AB respectively. If ar (ΔABC) = 16cm2, then ar (trapezium FBCE) =
Options
4 cm2
8 cm2
12 cm2
10 cm2
Solution
Given: In ΔABC
(1) D is the midpoint of BC
(2) E is the midpoint of CA
(3) F is the midpoint of AB
(4) Area of ΔABC = 16 cm2
To find: The area of Trapezium FBCE
Calculation: Here we can see that in the given figure,
Area of trapezium FBCE = Area of ||gm FBDE + Area of ΔCDE
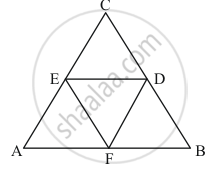
Since D and E are the midpoints of BC and AC respectively.
∴ DE || BA ⇒ DE || BF
Similarly, FE || BD. So BDEF is a parallelogram.
Now, DF is a diagonal of ||gm BDEF.
∴ Area of ΔBDF = Area of ΔDEF ……(1)
Similarly,
DE is a diagonal of ||gm DCEF
∴ Area of ΔDCE = Area of ΔDEF ……(2)
FE is the diagonal of ||gm AFDE
∴ Area of ΔAFE = Area of ΔDEF ……(3)
From (1), (2), (3) we have
Area of ΔBDF = Area of ΔDCF = Area of ΔAFE = Area of ΔDEF
But
Area of ΔBDF + Area of ΔDCE + Area of ΔAFE + Area of ΔDEF = Area of ΔABC
∴ 4 Area of ΔBDF = Area of ΔABC
Area of ΔBDF = `1/4` Area of ΔABC
= `1/4 (16)`
= 4 cm2
Area of ΔBDF = Area of ΔDCE = Area of ΔAFE = Area of ΔDEF = 4 cm2 …….(4)
Now
Area of trapezium FBCE = Area of || FBDE + Area of ΔCDE
=(Area of ΔBDF + Area of ΔDEF ) + Area of ΔCDE
= 4 + 4+ 4 (from 4)
= 12 cm2
Hence we get
Area of trapezium FBCE = 12 cm2
APPEARS IN
RELATED QUESTIONS
In fig below, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8
cm and CF = 10 cm, find AD.
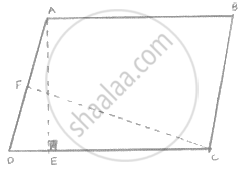
ABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove
that: (1) ar (ΔADO) = ar (ΔCDO) (2) ar (ΔABP) = ar (ΔCBP)
In the given figure, find the area of ΔGEF.
Diagonal AC and BD of trapezium ABCD, in which AB || DC, intersect each other at O. The triangle which is equal in area of ΔAOD is
Is the area of the blue shape more than the area of the yellow shape? Why?

Altogether how many squares can be arranged on it?
Measure the length of the floor of your classroom in meters. Also, measure the width.
- So how many children can sit in one square meter?
Cheggu’s wife asked him to make a circle with the wire. She knew it had an area of 800 square meters.
- Why did Cheggu not choose a rectangle? Explain.
Is the area of both your footprints the same?
Find the area of the following figure by counting squares:

