Advertisements
Advertisements
Question
ABCD is a parallelogram. P is any point on CD. If ar (ΔDPA) = 15 cm2 and ar (ΔAPC) = 20 cm2, then ar (ΔAPB) =
Options
15 cm2
20 cm2
35 cm2
30 cm2
Solution
Given: (1) ABCD is a parallelogram
(2) P is any point on CD
(3) Area of ΔDPA = 15 cm2
(4) Area of ΔAPC = 20 cm2
To find: Area of ΔAPB
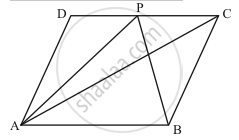
Calculation: We know that , “If a parallelogram and a a triangle are on the base between the same parallels, the area of triangle is equal to half the area of the parallelogram.”
Here , ΔAPB and ΔACB are on the same base and between the same parallels.
(since AC is the diagonal of parallelogram ABCD, diagonal of a parallelogram divides the parallelogram in two triangles of equal area)
ar (ΔACB ) = ar (ΔAPB)
ar (ΔACB) = ar (ΔADC)
ar (ΔACB) = Area of ΔADP + Area of ΔAPC
= 20 +15
= 35 cm2
Area of ΔACB = 35 cm2
APPEARS IN
RELATED QUESTIONS
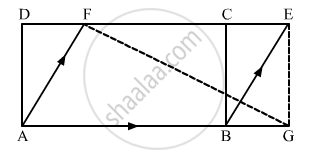
In the given figure, ABCD is a rectangle in which CD = 6 cm, AD = 8 cm. Find the area of parallelogram CDEF.

In the given figure, ABCD is a rectangle with sides AB = 10 cm and AD = 5 cm. Find the area of ΔEFG.
A, B, C, D are mid-points of sides of parallelogram PQRS. If ar (PQRS) = 36 cm2, then ar (ABCD) =
The figure obtained by joining the mid-points of the adjacent sides of a rectangle of sides 8 cm and 6 cm is ______.
ABCD is a trapezium with parallel sides AB =a and DC = b. If E and F are mid-points of non-parallel sides AD and BC respectively, then the ratio of areas of quadrilaterals ABFEand EFCD is
The side of a square field is 16 m. What will be increase in its area, if each of its sides is doubled?
By counting squares, estimate the area of the figure.

Is the area of your belt the same as the area of the postcard? Why or why not?
Nasreena is a farmer who wants to divide her land equally among her three children — Chumki, Jhumri, and Imran. She wants to divide the land so that each piece of land has one tree. Her land looks like this.
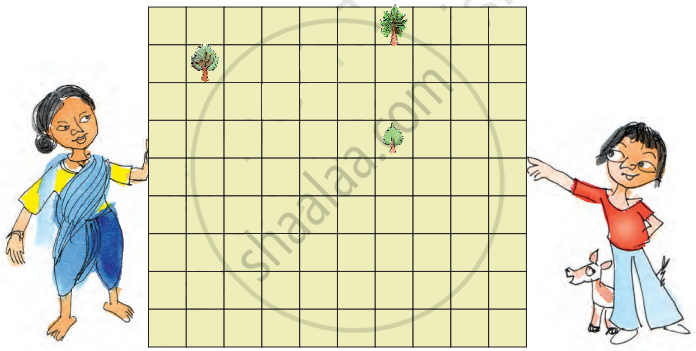
- Can you divide the land equally? Show how you will divide it. Remember each person has to get a tree. Colour each person’s piece of land differently.
Find the area of the following figure by counting squares:

