Advertisements
Advertisements
Question
ABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove
that: (1) ar (ΔADO) = ar (ΔCDO) (2) ar (ΔABP) = ar (ΔCBP)
Solution
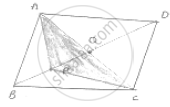
Given that ABCD is a parallelogram
To prove: (1) ar (ΔADO) = ar (ΔCDO)
(2) ar ( ΔABP) = ar (ΔCBP)
Then area (ΔADO) = area (ΔCDO)
Then; area (ΔBAO) area (ΔBCO) ......(1)
In a ΔPAC, Since PO is a median
Then, area (ΔPAO) = area (ΔPCO) ......(2)
⇒ Area (ΔABP) = Area of ΔCBP
APPEARS IN
RELATED QUESTIONS
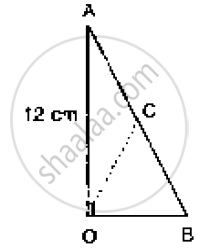
In the below fig. ∠AOB = 90°, AC = BC, OA = 12 cm and OC = 6.5 cm. Find the area of
ΔAOB.
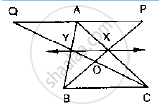
In the below fig. X and Y are the mid-points of AC and AB respectively, QP || BC and
CYQ and BXP are straight lines. Prove that ar (Δ ABP) = ar (ΔACQ).
P is any point on base BC of ΔABC and D is the mid-point of BC. DE is drawn parallel toPA to meet AC at E. If ar (ΔABC) = 12 cm2, then find area of ΔEPC.
The median of a triangle divides it into two ______.
In a ΔABC, D, E, F are the mid-points of sides BC, CA and AB respectively. If ar (ΔABC) = 16cm2, then ar (trapezium FBCE) =
The sides of a rectangular park are in the ratio 4 : 3. If its area is 1728 m2, find
(i) its perimeter
(ii) cost of fencing it at the rate of ₹40 per meter.
What will happen to the area of a rectangle, if its length and breadth both are trebled?
Find the area and perimeter of the following parallelograms
The region given in the following figure is measured by taking  as a unit. What is the area of the region?
as a unit. What is the area of the region?
Find the area of the following figure by counting squares:

