Advertisements
Advertisements
Question
A point D is taken on the side BC of a ΔABC such that BD = 2DC. Prove that ar(Δ ABD) =
2ar (ΔADC).
Solution
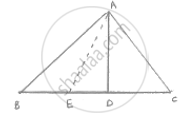
GIven that ,
In ΔABC, BD = 2 DC
To prove: ar ( ΔABD ) = 2ar (ΔADC)
Construction: Take a point E on BD such that BE = ED
Proof : Since, BE = ED and 2 BD = 2DC
Then, BE = ED = DC
We know that median of Δledivides it into two equal Δles
∴ In , ΔABD , AE is a median
Then, area (ΔABD) 2ar (ΔAED) .....(1)
In , ΔAEC , AD is a median
Then area (ΔAED) = area (ΔADC) ...... (2)
Compare equation (1) and (2)
Area (ΔABD) = 2ar (ΔADC).
APPEARS IN
RELATED QUESTIONS
If ABCD is a parallelogram, then prove that
𝑎𝑟 (Δ𝐴𝐵𝐷) = 𝑎𝑟 (Δ𝐵𝐶𝐷) = 𝑎𝑟 (Δ𝐴𝐵𝐶) = 𝑎𝑟 (Δ𝐴𝐶𝐷) = `1/2` 𝑎𝑟 (||𝑔𝑚 𝐴𝐵𝐶𝐷) .
In the given figure, find the area of ΔGEF.
A triangle and a parallelogram are on the same base and between the same parallels. The ratio of the areas of triangle and parallelogram is
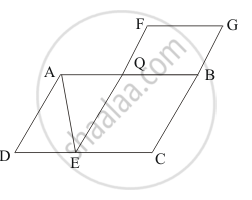
In the given figure, ABCD and FECG are parallelograms equal in area. If ar (ΔAQE) = 12 cm2, then ar (||gm FGBQ) =
The diagonal of a rectangular board is 1 m and its length is 96 cm. Find the area of the board.
Length of a rectangle is 30 m and its breadth is 20 m. Find the increase in its area if its length is increased by 10 m and its breadth is doubled.
The table given below contains some measures of the rectangle. Find the unknown values.
| Length | Breadth | Perimeter | Area |
| 13 cm | ? | 54 cm | ? |
What is the area of the rectangle? ________ square cm
Look at the table. If you were to write the area of each of these which column would you choose? Make a (✓).
| Square cm |
Square meter |
Square km |
|
| Handkerchief | ✓ | ||
| Sari | |||
| Page of your book | |||
| School land | |||
| Total land of a city | |||
| Door of your classroom | |||
| Chair seat | |||
| Blackboard | |||
| Indian flag | |||
| Land over which a river flows |
The amount of region enclosed by a plane closed figure is called its ______.
