Advertisements
Advertisements
Question
The diagonal of a rectangular board is 1 m and its length is 96 cm. Find the area of the board.
Solution
Length of diagonal (AB) = 96 cm
Diagonal (AC) = 1 m = 100 cm
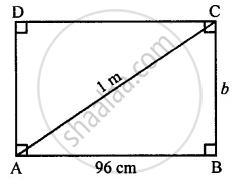
In right-angled triangle ABC,
By Applying Pythagoras Theorem,
(AC)2 = (AB)2 + (BC)2
= (100)2 = (96)2 + BC2
10000 = 9216 = BC2
10000 − 9216 = BC2
`sqrt784` = BC
∴ BC = 28 cm
Area of the rectangular board
= l × b or AB × BC
= 96 × 28
= 2688 cm2
APPEARS IN
RELATED QUESTIONS
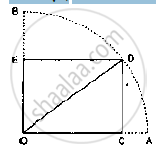
In the below fig. OCDE is a rectangle inscribed in a quadrant of a circle of radius 10 cm. If
OE = 2√5, find the area of the rectangle.
If ABC and BDE are two equilateral triangles such that D is the mid-point of BC, then find ar (ΔABC) : ar (ΔBDE).
In square ABCD, P and Q are mid-point of AB and CD respectively. If AB = 8cm and PQand BD intersect at O, then find area of ΔOPB.
Medians of ΔABC intersect at G. If ar (ΔABC) = 27 cm2, then ar (ΔBGC) =
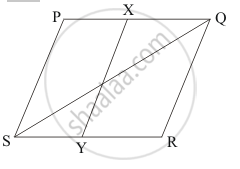
In the given figure, PQRS is a parallelogram. If X and Y are mid-points of PQ and SRrespectively and diagonal Q is joined. The ratio ar (||gm XQRY) : ar (ΔQSR) =
Find the area of a square, whose side is: 4.5 cm.
Altogether how many squares can be arranged on it?
So the area of piece A = ________ square cm
Find the area of the following figure by counting squares:

Find the area of the following figure by counting squares:

