Advertisements
Advertisements
Question
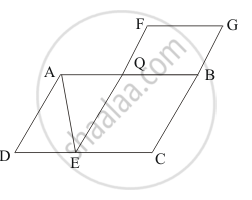
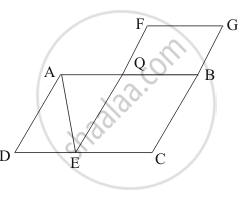
In the given figure, ABCD and FECG are parallelograms equal in area. If ar (ΔAQE) = 12 cm2, then ar (||gm FGBQ) =
Options
12 cm2
20 cm2
24 cm2
36 cm2
Solution
Given: (1) Area of parallelogram ABCD is equal to Area of parallelogram FECG.
(2) If Area of ΔAQE is 12cm.
To find: Area of parallelogram FGBQ
Calculation: We know that diagonal of a parallelogram divides the parallelogram into two triangles of equal area.
It is given that,
`ar ("||"^(gm)ABCD) = ar ("||"^(gm) FECG)`
`⇒ ar (ΔADE) + ar (ΔAQE) + ar ( "||"^(gm) QECB ) = ar ("||"^(gm) QECB) + ar ("||"^(gm) FQBG)`
`⇒ ar (ΔADE) + ar (ΔAQE) = ar "||"^(gm) FQBG`
`⇒ 2ar (ΔAQE) = ar ( "||"^(gm) FQBG)`
`⇒ar ( "||"^(gm) FQBG) = 2ar (ΔAQE) `
`⇒ar ( "||"^(gm) FQBG) = 2 xx 12`
`⇒ar ( "||"^(gm) FQBG) = 24 cm^2`
APPEARS IN
RELATED QUESTIONS
If ABCD is a parallelogram, then prove that
𝑎𝑟 (Δ𝐴𝐵𝐷) = 𝑎𝑟 (Δ𝐵𝐶𝐷) = 𝑎𝑟 (Δ𝐴𝐵𝐶) = 𝑎𝑟 (Δ𝐴𝐶𝐷) = `1/2` 𝑎𝑟 (||𝑔𝑚 𝐴𝐵𝐶𝐷) .
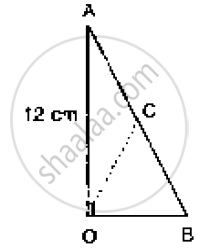
In the below fig. ∠AOB = 90°, AC = BC, OA = 12 cm and OC = 6.5 cm. Find the area of
ΔAOB.
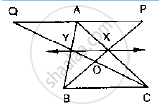
In the below fig. X and Y are the mid-points of AC and AB respectively, QP || BC and
CYQ and BXP are straight lines. Prove that ar (Δ ABP) = ar (ΔACQ).
In the given figure, ABCD is a parallelogram. If AB = 12 cm, AE = 7.5 cm, CF = 15 cm, then AD =

The mid-points of the sides of a triangle ABC along with any of the vertices as the fourth point make a parallelogram of area equal to ______.
Each side of a square is 7 m. If its each side be increased by 3 m, what will be the increase in its area.
Is the area of your belt the same as the area of the postcard? Why or why not?
Nasreena is a farmer who wants to divide her land equally among her three children — Chumki, Jhumri, and Imran. She wants to divide the land so that each piece of land has one tree. Her land looks like this.
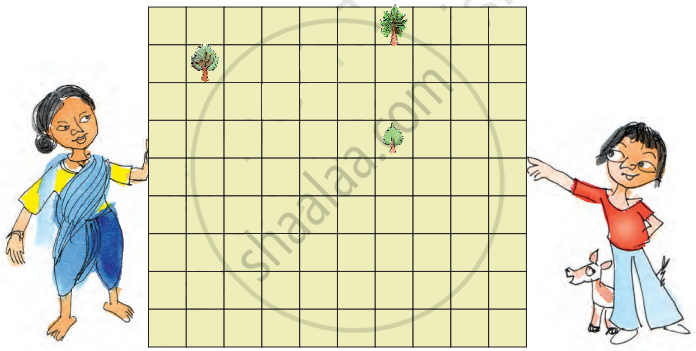
- Can you divide the land equally? Show how you will divide it. Remember each person has to get a tree. Colour each person’s piece of land differently.
An engineer who plans to build a compound wall on all sides of a house must find the area of the compound.
The region given in the following figure is measured by taking  as a unit. What is the area of the region?
as a unit. What is the area of the region?
