Advertisements
Advertisements
प्रश्न
A point D is taken on the side BC of a ΔABC such that BD = 2DC. Prove that ar(Δ ABD) =
2ar (ΔADC).
उत्तर
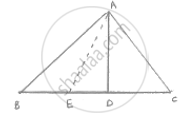
GIven that ,
In ΔABC, BD = 2 DC
To prove: ar ( ΔABD ) = 2ar (ΔADC)
Construction: Take a point E on BD such that BE = ED
Proof : Since, BE = ED and 2 BD = 2DC
Then, BE = ED = DC
We know that median of Δledivides it into two equal Δles
∴ In , ΔABD , AE is a median
Then, area (ΔABD) 2ar (ΔAED) .....(1)
In , ΔAEC , AD is a median
Then area (ΔAED) = area (ΔADC) ...... (2)
Compare equation (1) and (2)
Area (ΔABD) = 2ar (ΔADC).
APPEARS IN
संबंधित प्रश्न
If AD is a median of a triangle ABC, then prove that triangles ADB and ADC are equal in
area. If G is the mid-point of median AD, prove that ar (Δ BGC) = 2 ar (Δ AGC).
PQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm. A is any point on PQ. If PS = 5 cm, then find ar (ΔRAS)
The perimeter of a triangle ABC is 37 cm and the ratio between the lengths of its altitudes be 6: 5: 4. Find the lengths of its sides.
Let the sides be x cm, y cm, and (37 - x - y) cm. Also, let the lengths of altitudes be 6a cm, 5a cm, and 4a cm.
Find the area of a rectangle whose length = 3.6 m breadth = 90 cm
Each side of a square is 7 m. If its each side be increased by 3 m, what will be the increase in its area.
Length of a rectangle is 30 m and its breadth is 20 m. Find the increase in its area if its length is increased by 10 m and its breadth is doubled.
The table given below contains some measures of the rectangle. Find the unknown values.
| Length | Breadth | Perimeter | Area |
| 13 cm | ? | 54 cm | ? |
Is the area of your belt the same as the area of the postcard? Why or why not?
The King was very happy with carpenters Cheggu and Anar. They had made a very big and beautiful bed for him. So as gifts the king wanted to give some land to Cheggu, and some gold to Anar. Cheggu was happy. He took 100 meters of wire and tried to make different rectangles.
He made a 10 m × 40 m rectangle. Its area was 400 square meters. So he next made a 30 m × 20 m rectangle.
- What other rectangles can he make with 100 meters of wire? Discuss which of these rectangles will have the biggest area.
Find the area of the following figure by counting squares: