Advertisements
Advertisements
प्रश्न
The King was very happy with carpenters Cheggu and Anar. They had made a very big and beautiful bed for him. So as gifts the king wanted to give some land to Cheggu, and some gold to Anar. Cheggu was happy. He took 100 meters of wire and tried to make different rectangles.
He made a 10 m × 40 m rectangle. Its area was 400 square meters. So he next made a 30 m × 20 m rectangle.
- What other rectangles can he make with 100 meters of wire? Discuss which of these rectangles will have the biggest area.
उत्तर
Following rectangles are possible:
5 m × 45 m = 225 square m
15 m × 35 m = 525 square m
25 m × 25 m = 625 square m
The square will have the biggest area.
APPEARS IN
संबंधित प्रश्न
Let ABCD be a parallelogram of area 124 cm2. If E and F are the mid-points of sides AB and
CD respectively, then find the area of parallelogram AEFD.
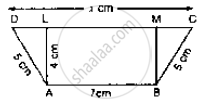
In the below fig. ABCD is a trapezium in which AB = 7 cm, AD = BC = 5 cm, DC = x cm,
and distance between AB and DC is 4cm. Find the value of x and area of trapezium ABCD.
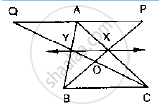
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that:
ar(ΔAPB) × ar(ΔCPD) = ar(ΔAPD) × ar (ΔBPC)
In the below Fig, ABC and ABD are two triangles on the base AB. If line segment CD is
bisected by AB at O, show that ar (Δ ABC) = ar (Δ ABD)

D is the mid-point of side BC of ΔABC and E is the mid-point of BD. if O is the mid-point
of AE, prove that ar (ΔBOE) = `1/8` ar (Δ ABC).
In the below fig. X and Y are the mid-points of AC and AB respectively, QP || BC and
CYQ and BXP are straight lines. Prove that ar (Δ ABP) = ar (ΔACQ).
If ABC and BDE are two equilateral triangles such that D is the mid-point of BC, then find ar (ΔABC) : ar (ΔBDE).
ABC is a triangle in which D is the mid-point of BC. E and F are mid-points of DC and AErespectively. IF area of ΔABC is 16 cm2, find the area of ΔDEF.
PQRS is a trapezium having PS and QR as parallel sides. A is any point on PQ and B is a point on SR such that AB || QR. If area of ΔPBQ is 17cm2, find the area of ΔASR.
The median of a triangle divides it into two ______.
In a ΔABC, D, E, F are the mid-points of sides BC, CA and AB respectively. If ar (ΔABC) = 16cm2, then ar (trapezium FBCE) =
The figure obtained by joining the mid-points of the adjacent sides of a rectangle of sides 8 cm and 6 cm is ______.
Medians of ΔABC intersect at G. If ar (ΔABC) = 27 cm2, then ar (ΔBGC) =
In a ΔABC if D and E are mid-points of BC and AD respectively such that ar (ΔAEC) = 4cm2, then ar (ΔBEC) =
In the given figure, ABCD is a parallelogram. If AB = 12 cm, AE = 7.5 cm, CF = 15 cm, then AD =

Diagonal AC and BD of trapezium ABCD, in which AB || DC, intersect each other at O. The triangle which is equal in area of ΔAOD is
ABCD is a trapezium in which AB || DC. If ar (ΔABD) = 24 cm2 and AB = 8 cm, then height of ΔABC is
The side of a square is 3.6 cm; find its area.
The side of a square field is 16 m. What will be increase in its area, if each of its sides is doubled?
Which has the bigger area - one of your footprints or the page of this book?
Which has the smaller area - two five-rupee notes together or a hundred rupee notes?
So the area of piece A = ________ square cm
In the same way, find the area of piece B.
An engineer who plans to build a compound wall on all sides of a house must find the area of the compound.
How will you decide? Discuss.
Find the area of the following figure by counting squares:

Find the area of the following figure by counting squares:

Find the area of the following figure by counting squares:

