Advertisements
Advertisements
प्रश्न
If ABC and BDE are two equilateral triangles such that D is the mid-point of BC, then find ar (ΔABC) : ar (ΔBDE).
उत्तर
Given: (1) ΔABC is equilateral triangle.
(2) ΔBDE is equilateral triangle.
(3) D is the midpoint of BC.
To find: ar (Δ ABC ) : ar (ΔBDE)
PROOF : Let us draw the figure as per the instruction given in the question.
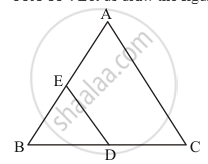
We know that area of equilateral triangle = `sqrt(3)/4 xx a^2`, where a is the side of the triangle.
Let us assume that length of BC is a cm.
This means that length of BD is `a/2` cm, Since D is the midpoint of BC.
∴ area of equilateral Δ ABC =`sqrt(3)/4 xx a^2` ------(1)
area of equilateral ΔBDE = `sqrt(3)/4 xx (a/2)^2` ------(2)
Now, ar(ΔABC) : ar(ΔBDE) =` sqrt(3)/4 xx a^2 : sqrt(3)/4 xx (a/2)^2` (from 1 and 2)
= 4 : 1
Hence we get the result ar(ΔABC) : ar(ΔBDE) = 4 : 1
APPEARS IN
संबंधित प्रश्न
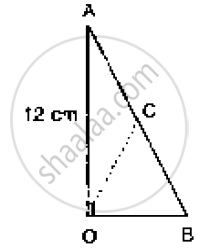
In the below fig. ∠AOB = 90°, AC = BC, OA = 12 cm and OC = 6.5 cm. Find the area of
ΔAOB.
If P is any point in the interior of a parallelogram ABCD, then prove that area of the
triangle APB is less than half the area of parallelogram.
A point D is taken on the side BC of a ΔABC such that BD = 2DC. Prove that ar(Δ ABD) =
2ar (ΔADC).
ABC is a triangle in which D is the mid-point of BC. E and F are mid-points of DC and AErespectively. IF area of ΔABC is 16 cm2, find the area of ΔDEF.
A triangle and a parallelogram are on the same base and between the same parallels. The ratio of the areas of triangle and parallelogram is
The median of a triangle divides it into two ______.
The figure obtained by joining the mid-points of the adjacent sides of a rectangle of sides 8 cm and 6 cm is ______.
The side of a square is 3.6 cm; find its area.
The King was very happy with carpenters Cheggu and Anar. They had made a very big and beautiful bed for him. So as gifts the king wanted to give some land to Cheggu, and some gold to Anar. Cheggu was happy. He took 100 meters of wire and tried to make different rectangles.
He made a 10 m × 40 m rectangle. Its area was 400 square meters. So he next made a 30 m × 20 m rectangle.
- What other rectangles can he make with 100 meters of wire? Discuss which of these rectangles will have the biggest area.
Find the area of the following figure by counting squares:

