Advertisements
Advertisements
प्रश्न
If ABC and BDE are two equilateral triangles such that D is the mid-point of BC, then find ar (ΔABC) : ar (ΔBDE).
उत्तर
Given: (1) ΔABC is equilateral triangle.
(2) ΔBDE is equilateral triangle.
(3) D is the midpoint of BC.
To find: ar (Δ ABC ) : ar (ΔBDE)
PROOF : Let us draw the figure as per the instruction given in the question.
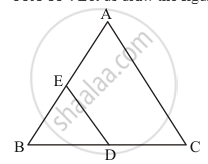
We know that area of equilateral triangle = `sqrt(3)/4 xx a^2`, where a is the side of the triangle.
Let us assume that length of BC is a cm.
This means that length of BD is `a/2` cm, Since D is the midpoint of BC.
∴ area of equilateral Δ ABC =`sqrt(3)/4 xx a^2` ------(1)
area of equilateral ΔBDE = `sqrt(3)/4 xx (a/2)^2` ------(2)
Now, ar(ΔABC) : ar(ΔBDE) =` sqrt(3)/4 xx a^2 : sqrt(3)/4 xx (a/2)^2` (from 1 and 2)
= 4 : 1
Hence we get the result ar(ΔABC) : ar(ΔBDE) = 4 : 1
APPEARS IN
संबंधित प्रश्न
In Q. No 1, if AD = 6 cm, CF = 10 cm, and AE = 8cm, find AB.
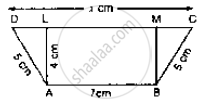
In the below fig. ABCD is a trapezium in which AB = 7 cm, AD = BC = 5 cm, DC = x cm,
and distance between AB and DC is 4cm. Find the value of x and area of trapezium ABCD.
A point D is taken on the side BC of a ΔABC such that BD = 2DC. Prove that ar(Δ ABD) =
2ar (ΔADC).
In the given figure, find the area of ΔGEF.
In square ABCD, P and Q are mid-point of AB and CD respectively. If AB = 8cm and PQand BD intersect at O, then find area of ΔOPB.
The area of the figure formed by joining the mid-points of the adjacent sides of a rhombus with diagonals 16 cm and 12 cm is
ABCD is a trapezium in which AB || DC. If ar (ΔABD) = 24 cm2 and AB = 8 cm, then height of ΔABC is
ABCD is a rectangle with O as any point in its interior. If ar (ΔAOD) = 3 cm2 and ar (ΔABOC) = 6 cm2, then area of rectangle ABCD is
Cheggu’s wife asked him to make a circle with the wire. She knew it had an area of 800 square meters.
- Why did Cheggu not choose a rectangle? Explain.
Area of a rectangle with length 5 cm and breadth 3 cm is ______.
