Advertisements
Advertisements
प्रश्न
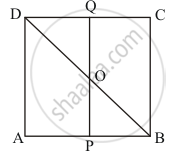
In square ABCD, P and Q are mid-point of AB and CD respectively. If AB = 8cm and PQand BD intersect at O, then find area of ΔOPB.
उत्तर
Given: Here from the given question we get
(1) ABCD is a square,
(2) P is the midpoint of AB
(3) Q is the midpoint of CD
(4) PQ and BD intersect at O.
(5) AB = 8cm
To find : Area of ΔOPB
Calculation: Since P is the midpoint of AB,
`BP = 1/2 (AB) `
= 1/2 (8)`
= 4 cm
BP = 4cm ……(1)
Area of triangle = `1/2 `× base × height
Area of ΔOPB = `1/2` × BP × PO (from 1)
` = 1/2 × 4 × (PO = 1/2 AD , APQD ` is a rectangle)
`= 1/2 × 16 `
Area of ΔOPB = 8 cm2
Hence we get the Area of ΔOBP = 8 cm2
APPEARS IN
संबंधित प्रश्न
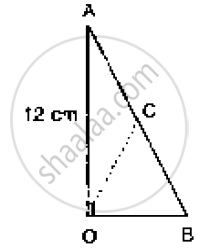
In the below fig. ∠AOB = 90°, AC = BC, OA = 12 cm and OC = 6.5 cm. Find the area of
ΔAOB.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that:
ar(ΔAPB) × ar(ΔCPD) = ar(ΔAPD) × ar (ΔBPC)
PQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm. A is any point on PQ. If PS = 5 cm, then find ar (ΔRAS)
A triangle and a parallelogram are on the same base and between the same parallels. The ratio of the areas of triangle and parallelogram is
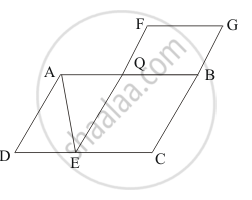
In the given figure, ABCD and FECG are parallelograms equal in area. If ar (ΔAQE) = 12 cm2, then ar (||gm FGBQ) =
The table given below contains some measures of the rectangle. Find the unknown values.
| Length | Breadth | Perimeter | Area |
| ? | 15 cm | 60 cm | ? |
The King was very happy with carpenters Cheggu and Anar. They had made a very big and beautiful bed for him. So as gifts the king wanted to give some land to Cheggu, and some gold to Anar. Cheggu was happy. He took 100 meters of wire and tried to make different rectangles.
He made a 10 m × 40 m rectangle. Its area was 400 square meters. So he next made a 30 m × 20 m rectangle.
- What other rectangles can he make with 100 meters of wire? Discuss which of these rectangles will have the biggest area.
Whose footprint is larger - yours or your friend’s?
Find the area of the following figure by counting squares:

Find the area of the following figure by counting squares:

