Advertisements
Advertisements
प्रश्न
ABC is a triangle in which D is the mid-point of BC. E and F are mid-points of DC and AErespectively. IF area of ΔABC is 16 cm2, find the area of ΔDEF.
उत्तर
Given: Here from the given question we get
(1) ABC is a triangle
(2) D is the midpoint of BC
(3) E is the midpoint of CD
(4) F is the midpoint of A
Area of ΔABC = 16 cm2
To find : Area of ΔDEF
Calculation: We know that ,
The median divides a triangle in two triangles of equal area.
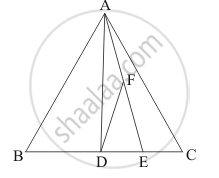
For ΔABC, AD is the median
Area of Δ ADC = `1/2 `(Area of ΔABC )
`=1/2 (16)`
= 8 cm2
Area of Δ ADC = 8cm2
For ΔADC , AE is the median .
Area of ΔAED = `1/2 ` (Area of Δ ABC)
`= 1/2 (8)`
= 4 cm2
Area of ΔAED = 4 cm2
Similarly, For ΔAED , DF is the median .
Area of ΔDEF = `1/2 ` (Area of Δ AED)
`= 1/2 (4)`
= 2 cm2
Area of ΔDEF = 2 cm2
Hence we get Area of ΔDEF = 2 cm2
APPEARS IN
संबंधित प्रश्न
ABCD is a parallelogram. E is a point on BA such that BE = 2 EA and F is a point on DC
such that DF = 2 FC. Prove that AE CF is a parallelogram whose area is one third of the
area of parallelogram ABCD.
In the given figure, ABCD is a rectangle in which CD = 6 cm, AD = 8 cm. Find the area of parallelogram CDEF.

The length and breadth of a rectangular piece of land are in the ratio 5 : 3. If the total cost of fencing it at the rate of ₹24 per meter is ₹9600, find its :
(i) length and breadth
(ii) area
(iii) cost of levelling at the rate of ₹60 per m2.
Find the area of a rectangle whose length = 15 cm breadth = 6.4 cm
By counting squares, estimate the area of the figure.

Look at a 10 rupee note. Is its area more than hundred square cm?
Cheggu’s wife asked him to make a circle with the wire. She knew it had an area of 800 square meters.
- Why did Cheggu not choose a rectangle? Explain.
Karunya bought three fields.
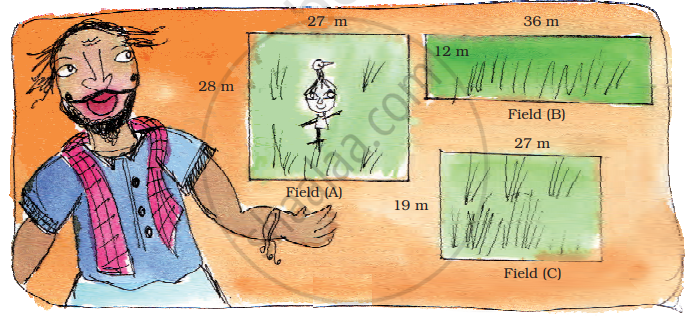
Find the area of all three fields.
- Field (A) ____________ square metre.
- Field (B) ____________ square metre.
- Field (C) ____________ square metre.
An engineer who plans to build a compound wall on all sides of a house must find the area of the compound.
Find all the possible dimensions (in natural numbers) of a rectangle with a perimeter 36 cm and find their areas.
