Advertisements
Advertisements
प्रश्न
If AD is a median of a triangle ABC, then prove that triangles ADB and ADC are equal in
area. If G is the mid-point of median AD, prove that ar (Δ BGC) = 2 ar (Δ AGC).
उत्तर

Draw AM ⊥ BC
Since, AD is the median of ΔABC
∴ BD = DC
⇒ BD = AM = DC × AM
⇒ ` 1/2 (BD xx AM ) = 1/2 ( DC xx AM)`
⇒ ar (Δ ABC) = ar (Δ ACD) ........ (1)
In ΔBGC , GDis the median
∴ ar (BGD) = area (OGD) ......... (2)
In ΔACD , CG is the median
∴ area (AGC) = area (Δ CGD) ......... (3)
From (1) and (2) , we have
Area (ΔBGD) = ar (Δ AGC)
But, ar (ΔBGC) = 2ar (BGD)
∴ ar (BGC ) = 2ar (Δ AGC)
APPEARS IN
संबंधित प्रश्न
ABCD is a parallelogram whose diagonals AC and BD intersect at O. A line through O
intersects AB at P and DC at Q. Prove that ar (Δ POA) = ar (Δ QOC).
In square ABCD, P and Q are mid-point of AB and CD respectively. If AB = 8cm and PQand BD intersect at O, then find area of ΔOPB.
If AD is median of ΔABC and P is a point on AC such that
ar (ΔADP) : ar (ΔABD) = 2 : 3, then ar (Δ PDC) : ar (Δ ABC)
ABCD is a rectangle with O as any point in its interior. If ar (ΔAOD) = 3 cm2 and ar (ΔABOC) = 6 cm2, then area of rectangle ABCD is
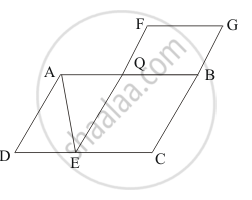
In the given figure, ABCD and FECG are parallelograms equal in area. If ar (ΔAQE) = 12 cm2, then ar (||gm FGBQ) =
The sides of a rectangular park are in the ratio 4 : 3. If its area is 1728 m2, find
(i) its perimeter
(ii) cost of fencing it at the rate of ₹40 per meter.
The side of a square field is 16 m. What will be increase in its area, if each of its sides is increased by 4 m?
Look at a 10 rupee note. Is its area more than hundred square cm?
Each line gives a story. You have to choose the question which makes the best story problem. The first one is already marked.
- 352 children from a school went on a camping trip. Each tent had a group of 4 children.
a) How many children did each tent have? b) How many tents do they need? c) How many children in all are in the school?
Find the area of the following figure by counting squares:

