Advertisements
Advertisements
प्रश्न
If AD is a median of a triangle ABC, then prove that triangles ADB and ADC are equal in
area. If G is the mid-point of median AD, prove that ar (Δ BGC) = 2 ar (Δ AGC).
Advertisements
उत्तर
Draw AM ⊥ BC
Since, AD is the median of ΔABC
∴ BD = DC
⇒ BD = AM = DC × AM
⇒ ` 1/2 (BD xx AM ) = 1/2 ( DC xx AM)`
⇒ ar (Δ ABC) = ar (Δ ACD) ........ (1)
In ΔBGC , GDis the median
∴ ar (BGD) = area (OGD) ......... (2)
In ΔACD , CG is the median
∴ area (AGC) = area (Δ CGD) ......... (3)
From (1) and (2) , we have
Area (ΔBGD) = ar (Δ AGC)
But, ar (ΔBGC) = 2ar (BGD)
∴ ar (BGC ) = 2ar (Δ AGC)
APPEARS IN
संबंधित प्रश्न
ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects
CD at F.
(i) Prove that ar (ΔADF) = ar (ΔECF)
(ii) If the area of ΔDFB = 3 cm2, find the area of ||gm ABCD.
ABCD is a rectangle with O as any point in its interior. If ar (ΔAOD) = 3 cm2 and ar (ΔABOC) = 6 cm2, then area of rectangle ABCD is
Find the area of a square, whose side is: 4.1 cm.
By counting squares, estimate the area of the figure.
Altogether how many squares can be arranged on it?
Look at the table. If you were to write the area of each of these which column would you choose? Make a (✓).
| Square cm |
Square meter |
Square km |
|
| Handkerchief | ✓ | ||
| Sari | |||
| Page of your book | |||
| School land | |||
| Total land of a city | |||
| Door of your classroom | |||
| Chair seat | |||
| Blackboard | |||
| Indian flag | |||
| Land over which a river flows |
Karunya bought three fields.
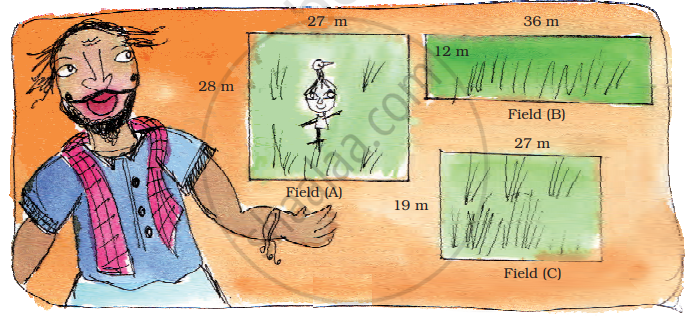
Find the area of all three fields.
- Field (A) ____________ square metre.
- Field (B) ____________ square metre.
- Field (C) ____________ square metre.
Find the area of the following figure by counting squares:
Find the area of the following figure by counting squares:
If a figure contains only 8 fully-filled squares and no partial squares, what is its area?
